单选题 (共 10 题 ),每题只有一个选项正确
已知函数 $f(x)=\int_0^x e^{\cos t} d t, g(x)=\int_0^{\sin x} e^{t^2} d t$, 则
$\text{A.}$ $f(x)$ 是奇函数, $g(x)$ 是偶函数
$\text{B.}$ $f(x)$ 足偶函数, $g(x)$ 足奇函数
$\text{C.}$ $f(x)$ 与 $g(x)$ 均为奇函数
$\text{D.}$ $f(x)$ 与 $g(x)$ 均为周期函数
设 $P=P(x, y, z) , Q=Q(x, y, z)$ 均为连续函数, $\sum$ 为曲面 $Z=\sqrt{1-x^2-y^2}(x \leq 0, y \geq 0)$ 的上侧, 则 $\iint_{\Sigma} P d y d z+Q d z d x=$
$\text{A.}$ $\iint_{\Sigma}\left(\frac{x}{z} P+\frac{y}{z} Q\right) d x d y$
$\text{B.}$ $\iint_{\Sigma}\left(-\frac{x}{z} P+\frac{y}{z} Q\right) d x d y$
$\text{C.}$ $\iint_{\Sigma}\left(\frac{x}{z} P-\frac{y}{z} Q\right) d x d y$
$\text{D.}$ $\iint_{\Sigma}\left(-\frac{x}{z} P-\frac{y}{z} Q\right) d x d y$
已知幂级数 $\sum_{n=0}^{\infty} a_n x^n$ 的和函数为 $\ln (2+x)$, 则 $\sum_{n=0}^{\infty} n a_{2 n}=$
$\text{A.}$ $-\frac{1}{6}$
$\text{B.}$ $-\frac{1}{3}$
$\text{C.}$ $\frac{1}{6}$
$\text{D.}$ $\frac{1}{3}$
设函数 $f(x)$ 在区间 $(-1,1)$ 上有定义, 且 $\lim _{x \rightarrow 0} f(x)=0$, 则
$\text{A.}$ 当 $\lim _{x \rightarrow 0} \frac{f(x)}{x}=m$ 时, $f^{\prime}(0)=m$
$\text{B.}$ 当 $f^{\prime}(0)=m$ 时, $\lim _{x \rightarrow 0} \frac{f(x)}{x}=m$
$\text{C.}$ 当 $\lim _{x \rightarrow 0} f^{\prime}(x)=m$ 时, $f^{\prime}(0)=m$
$\text{D.}$ 当 $f^{\prime}(0)=m$ 时, $\lim _{x \rightarrow 0} f^{\prime}(x)=m$
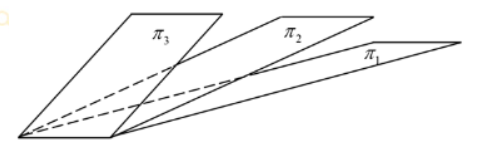
在空间直角坐标系 $O-x y z$ 中, 三张平面 $\pi_i: a_i x+b_i y+c_i z=d_i(i=1,2,3)$ 的位置关系如图所示,记 $\alpha_i=\left(a_i, b_i, c_i, d_i\right)$, 若 $r\left(\begin{array}{l}\alpha_1 \\ \alpha_2 \\ \alpha_3\end{array}\right)=m, r\left(\begin{array}{l}\beta_1 \\ \beta_2 \\ \beta_3\end{array}\right)=n$, 则
$\text{A.}$ $m=1, n=2$
$\text{B.}$ $m=n=2$
$\text{C.}$ $m=2, n=3$
$\text{D.}$ $m=n=3$
设向量 $\alpha_1=\left(\begin{array}{c}2 \\ 1 \\ -1 \\ 3\end{array}\right), \alpha_2=\left(\begin{array}{l}1 \\ 1 \\ b \\ a\end{array}\right), \alpha_3=\left(\begin{array}{c}1 \\ a \\ -1 \\ 1\end{array}\right)$, 若 $\alpha_1, \alpha_2, \alpha_3$ 线性相关, 且.其中两个向量均线性不相关, 则
$\text{A.}$ $a=1, b \neq 1$
$\text{B.}$ $a=1, b=-1$
$\text{C.}$ $a \neq 2, b=2$
$\text{D.}$ $a=-2, b=2$
设 $A$ 是秩为 2 的 3 阶矩阵, $\alpha$ 是满足 $A \alpha=0$ 的非零向量, 若对满足 $\beta^T \alpha=0$ 的 3 维向量 $A \beta=\beta$ 均有, 则
$\text{A.}$ $A^3$ 的迹为 2
$\text{B.}$ $A^3$ 的迹为 5
$\text{C.}$ $A^2$ 的迹为 8
$\text{D.}$ $A^2$ 的迹为 9
设随机变量 $\mathrm{X}$ 与 $\mathrm{Y}$ 独立, $\mathrm{X}$ 服从 $\mathrm{N}(0,2)$ 的正态分布, $\mathrm{Y}$ 服从 $\mathrm{N}(-2,2)$ 的正态分布, 若 $P\{2 X+Y < a\}=P\{X>Y\}$, 则 $a=$
$\text{A.}$ $-2-\sqrt{10}$
$\text{B.}$ $-2+\sqrt{10}$
$\text{C.}$ $-2-\sqrt{6}$
$\text{D.}$ $-2+\sqrt{6}$
设随机变量 $X$ 的概率密度为 $f(x)=\left\{\begin{array}{cc}2(1-x), & 0 < x < 1 \\ 0, & \text { 其它 }\end{array}\right.$, 在 $X=X(0 < x < 1)$ 的条件下, 随机变量 $Y$ 服从区间 $(x, 1)$ 上的均匀分布,则 $\operatorname{Cov}(X, Y)=$
$\text{A.}$ $-\frac{1}{36}$
$\text{B.}$ $-\frac{1}{72}$
$\text{C.}$ $\frac{1}{72}$
$\text{D.}$ $\frac{1}{36}$
设随机变量 $X, Y$ 相互独立, 且均服从参数为 $\lambda$ 的指数分布, 令 $Z=|X-Y|$, 则下列随机变量与 Z 同分布的是
$\text{A.}$ $X+Y$
$\text{B.}$ $\frac{X+Y}{2}$
$\text{C.}$ $2 \mathrm{X}$
$\text{D.}$ $X$
填空题 (共 6 题 ),请把答案直接填写在答题纸上
若 $\lim _{x \rightarrow 0} \frac{\left(1+a x^2\right)^{\sin x}-1}{x^3}=6$, 则 $a=$
设函数 $f(u, v)$ 具有 2 阶连续偏导数, 且 $\left.d f\right|_{(1,1)}=3 d u+4 d v$, 令 $y=f\left(\cos x, 1+x^2\right)$, 则 $\left.\frac{d^2 y}{d x^2}\right|_{x=0}=$
已知函数 $f(x)=x+1$, 若 $f(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty} a_n \cos n x, x \in[0, \pi]$, 则 $\lim _{n \rightarrow \infty} n^2 \sin a_{2 n-1}=$
微分方程 $y^{\prime}=\frac{1}{(x+y)^2}$ 满足条件 $y(1)=0$ 的解为
设实矩阵 $A=\left(\begin{array}{cc}a+1 & a \\ a & a\end{array}\right)$, 若对任意实向量 $\alpha=\left(\begin{array}{l}x_1 \\ x_2\end{array}\right), \beta=\left(\begin{array}{l}y_1 \\ y_2\end{array}\right)$, $\left(\alpha^T A \beta\right)^2 \leq \alpha^T A \alpha \cdot \beta^T A \beta$ 都成立, 则 $a$ 的取值范围是
设随机试验每次成功的概率为 $P$, 现进行 3 次独立重复试验, 在至少成功 1 次的条件下, 3 次试验全部成功的概率为 $\frac{4}{13}$, 则 $P=$
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知平面区域 $D=\left\{(x, y) \mid \sqrt{1-y^2} \leq x \leq 1,-1 \leq y \leq 1\right\}$, 计算 $\iint_D \frac{x}{\sqrt{x^2+y^2}} \mathrm{~d} \sigma$.
已知函数 $f(x, y)=x^3+y^3-(x+y)^2+3$, 设 $T$ 是曲面 $z=f(x, y)$在点 $(1,1,1)$ 处的切平面, $D$ 为 $T$ 与坐标平面所围成的有界区域在 $x O y$ 平面上的投影.
(1) 求 $T$ 的方程
(2) 求 $f(x, y)$ 在 $D$ 上的最大值和最小值
设函数 $f(x)$ 具有二阶导数,且 $f^{\prime}(0)=f^{\prime}(1),\left|f^{\prime \prime}(x)\right| \leq 1$. 证
(1) 当 $x \in(0,1)$ 时,有
$|f(x)-f(0)(1-x)-f(1) x| \leq \frac{x(1-x)}{2} ;$
(2) 证明: $\left|\int_0^1 f(x) \mathrm{d} x-\frac{f(0)+f(1)}{2}\right| \leq \frac{1}{12}$.
已知有向曲线 $\mathrm{L}$ 为球面 $\mathrm{x}^2+\mathrm{y}^2+\mathrm{z}^2=2 \mathrm{x}$ 与平面 $2 \mathrm{x}-\mathrm{z}-1=0$ 的交线从 $\mathrm{z}$ 轴正向往 $\mathrm{z}$ 轴负向看去为逆时针方向, 计算曲线积分 $\int_L\left(6 x y z-y z^2\right) d x+2 x^2 z d y+x y z d z$
已知数列 $\left\{x_n\right\} .\left\{y_n\right\} .\left\{z_n\right\}$ 满足 $x_0=-1, y_0=0, z_0=2$. 且 $\left\{\begin{array}{c}x_n=-2 x_{n-1}+2 z_{n-1} \\ y_n=-2 y_{n-1}-2 z_{n-1} \\ z_n=-6 x_{n-1}-3 y_{n-1}+3 z_{n-1}\end{array}\right.$,记 $\alpha_n=\left\{\begin{array}{l}x_n \\ y_n \\ z_n\end{array}\right\}$, 写出海足 $\alpha_n=A \alpha_{n-1}$ 的矩阵 $A$, 并求 $A^n$ 及 $x_n, y_n, z_n(n=1,2, \cdots)$.
设总体 $X$ 服从 $[0, \theta]$ 上的均匀分布, 其中 $\theta \in(0,+\infty)$ 为未知参数, $X_1, X_2, \cdots, X_n$ 是来自总体 $X$ 的简单随机样本, 记
$$
X(n)=\max \left\{X_1, X_2, \cdots, X_n\right\}, T_c=c X(n) .
$$
(1) 求 $c$, 使得 $T_c$ 是 $\theta$ 的无偏估计;
(2) 记 $h(c)=E\left(T_c-\theta\right)^2$, 求 $c$ 使得 $h(c)$ 最小.