单选题 （共 8 题 ），每题只有一个选项正确
已知函数 $f(x)$ 是 $R$ 上的偶函数, 当 $x \geq 0$ 时 $f(x)=\left\{\begin{array}{l}-x^2+1,0 \leq x < 1 \\ 2-2^x, x \geq 1\end{array}\right.$, 则 $f(-2)$ 的值为
$\text{A.}$ -3
$\text{B.}$ -2
$\text{C.}$ 2
$\text{D.}$ 3
已知函数 $f(x)$ 是 $R$ 上的偶函数, 且满足 $f(x)=f(x+4)$, 当 $x \in[0,2)$ 时, $y=\log _2(x+1)$, 则 $f(2019)+f(2020)=(\quad)$
$\text{A.}$ 1
$\text{B.}$ -1
$\text{C.}$ -2
$\text{D.}$ 2
" $a=1$ "是"函数 $f(x)=\log _2 \frac{a x+1}{x-1}$ 是奇函数"的
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 既不充分又不必要条件
已知 $f(x), g(x)$ 分别是定义在 $R$ 上的偶函数和奇函数, $f(x)-g(x)=x^3+x^2+a$, 则 $g(3)=(\quad)$
$\text{A.}$ 27
$\text{B.}$ -27
$\text{C.}$ -8
$\text{D.}$ 8
函数 $f(x)=\frac{\ln |x|}{\mathrm{e}^x+\mathrm{e}^{-x}}$ 的部分图象大致为
$\text{A.}$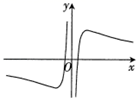 
$\text{B.}$ 
$\text{C.}$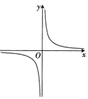 
$\text{D.}$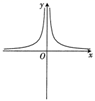 
设函数 $f(x)$ 的定义域为 $\mathrm{R}, f(2 x+1)$ 为奇函数, $f(x+2)$ 为偶函数, 当 $x \in[0,1]$ 时, $f(x)=a^x+b$.若 $f(0)+f(3)=-1$, 则
$\text{A.}$ $b=-1$
$\text{B.}$ $f(2023)=-1$
$\text{C.}$ $f(x)$ 为偶函数
$\text{D.}$ $f(x)$ 的图象关于 $\left(\frac{1}{2}, 0\right)$ 对称
已知函数 $f(x)$ 是定义在 $\mathbf{R}$ 上的奇函数, 且 $\forall x_1, x_2 \in[0,+\infty)$,有 $\left(x_1-x_2\right)\left[f\left(x_1\right)-f\left(x_2\right)\right] < 0$ 成立，若 $f(1)=-1$ ，则关于 $x$ 的不等式 $|f(x-1)| \leq 1$ 的解集是
$\text{A.}$ $[0,1]$
$\text{B.}$ $[0,2]$
$\text{C.}$ $[-1,1]$
$\text{D.}$ $[1,2]$
已知函数 $f(x)=\frac{1}{\mathrm{e}^x}-\mathrm{e}^x-2 x+4$, 其中 $e$ 是自然对数的底数, 若 $f(a-6)+f\left(a^2\right)>8$, 则实数 $a$ 的取值范围是
$\text{A.}$ $(2,+\infty)$
$\text{B.}$ $(-3,2)$
$\text{C.}$ $(-\infty,-3)$
$\text{D.}$ $(-\infty,-3) \mathrm{U}(2,+\infty)$
多选题 （共 4 题 ），每题有多个选项正确
函数 $f(x)$ 是定义在 $R$ 上的奇函数, 下列说法正确的是
$\text{A.}$ $f(0)=0$
$\text{B.}$ 若 $f(x)$ 在 $[0,+\infty)$ 上有最小值 -1 , 则 $f(x)$ 在 $(-\infty, 0]$ 上有最大值 1
$\text{C.}$ 若 $f(x)$ 在 $[1,+\infty)$ 上为增函数, 则 $f(x)$ 在 $(-\infty,-1]$ 上为减函数
$\text{D.}$ 若 $x>0$ 时, $f(x)=x^2-2 x$, 则 $x < 0$ 时, $f(x)=-x^2-2 x$
已知函数 $f(x)$ 的定义域为 $\mathbf{R}, f(x+2)$ 为奇函数, $f(2 x+1)$ 为偶函数, 则
$\text{A.}$ $f(x)$ 的图象关于直线 $x=1$ 对称
$\text{B.}$ $f(x)$ 的图象关于点 $(1,0)$ 对称
$\text{C.}$ $f(x)$ 的图象关于直线 $x=2$ 对称
$\text{D.}$ $f(x)$ 的图象关于点 $(2,0)$ 对称
已知函数 $f(x)$ 为 $\mathbf{R}$ 上的奇函数， $f(1+x)$ 为偶函数, 则
$\text{A.}$ $f(-2-x)+f(x)=0$
$\text{B.}$ $f(1-x)=f(1+x)$
$\text{C.}$ $f(x+2)=f(x-2)$
$\text{D.}$ $f(2023)=0$
已知函数 $f(x)$ 的定义域为 R , 函数 $f(x)$ 的图象关于点 $(1,0)$ 对称, 且满足 $f(x+3)=f(1-x)$, 则下列结论正确的是
$\text{A.}$ 函数 $f(x+1)$ 是奇函数
$\text{B.}$ 函数 $f(x)$ 的图象关于 $y$ 轴对称
$\text{C.}$ 函数 $f(x)$ 是最小正周期为 2 的周期函数
$\text{D.}$ 若函数 $g(x)$ 满足 $g(x)+f(x+3)=2$, 则 $\sum_{k=1}^{2024} g(k)=4048$
填空题 （共 4 题 ），请把答案直接填写在答题纸上
已知函数 $f(x)$ 满足: (1) $f(x)$ 为偶函数; (2) $f(x)$ 的图象过点 $(\mathrm{e}, 1)$; (3)对任意的非零实数 $x_1, x_2$, $f\left(\frac{x_1}{x_2}\right)=f\left(x_1\right)-f\left(x_2\right)$. 请写出一个满足上述条件的函数 $f(x)=$ $\qquad$ .
若函数 $f(x)=\ln \left(\mathrm{e}^x+1\right)^x+a x^2$ 是奇函数, 则实数 $a=$
已知函数 $y=f(x)$, 对任意 $x \in R$, 都有 $f(x+2) \cdot f(x)=k$ ( $k$ 为常数), 且当 $x \in[0,2]$ 时, $f(x)=x^2+1$,则 $f(2021)=$
已知函数 $f(x)$ 的定义域为 $\mathbf{R}, y=f(x)+\mathrm{e}^x$ 是偶函数, $y=f(x)-3 \mathrm{e}^x$ 是奇函数, 则 $f(x)$ 的最小值为