单选题 (共 8 题 ),每题只有一个选项正确
若 $f(x)=\left\{\begin{array}{cc}\frac{1-\cos \sqrt{x}}{a x} & , x>0 \\ b, & x \leq 0\end{array}\right.$ 在 $x=0$ 处连续, 则
$\text{A.}$ $a b=\frac{1}{2}$
$\text{B.}$ $a b=-\frac{1}{2}$
$\text{C.}$ $a b=0$
$\text{D.}$ $a b=2$
设函数 $f(x)$ 可导,且 $f(x) f^{\prime}(x)>0$ ,则
$\text{A.}$ $f(1)>f(-1)$
$\text{B.}$ $f(1) < f(-1)$
$\text{C.}$ $|f(1)|>|f(-1)|$
$\text{D.}$ $|f(1)| < |f(-1)|$
函数 $f(x, y, z)=x^2 y+z^2$ 在点 $(1,2,0)$ 处沿向量 $\vec{n}=(1,2,2)$ 的方向导数为
$\text{A.}$ 12
$\text{B.}$ 6
$\text{C.}$ 4
$\text{D.}$ 2
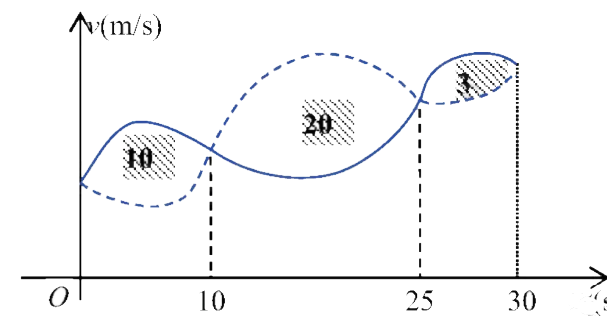
甲乙两人赛跑,计时开始时,甲在乙前方 10 (单位:m) 处.图中,实线表示甲的速度曲线 $v=v_1(t)$ (单位: $\mathrm{m} / \mathrm{s}$ )虚线表示乙的速度曲线 $v=v_2(t)$ ,三块阴影部分面积的数值依次为 $10 , 20 , 3$ ,计时开始后乙追上甲的时刻记为 $t_0$ (单位: $s$ ),则
$\text{A.}$ $t_0=10$
$\text{B.}$ $15 < t_0 < 20$
$\text{C.}$ $t_0=25$
$\text{D.}$ $t_0>25$
设 $\alpha$ 为 $n$ 维单位列向量, $E$ 为 $n$ 阶单位矩阵,则
$\text{A.}$ $E-\alpha \alpha^T$ 不可逆
$\text{B.}$ $E+\alpha \alpha^T$ 不可逆
$\text{C.}$ $E+2 \alpha \alpha^T$ 不可逆
$\text{D.}$ $E-2 \alpha \alpha^T$ 不可逆
已知矩阵 $A=\left[\begin{array}{lll}2 & 0 & 0 \\ 0 & 2 & 1 \\ 0 & 0 & 1\end{array}\right] , B=\left[\begin{array}{lll}2 & 1 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 1\end{array}\right]$ , $C=\left[\begin{array}{lll}1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2\end{array}\right]$ ,则
$\text{A.}$ $A$ 与 $C$ 相似, $B$ 与 $C$ 相似
$\text{B.}$ $A$ 与 $C$ 相似, $B$ 与 $C$ 不相似
$\text{C.}$ ${A}$ 与 $C$ 不相似, $B$ 与 $C$ 相似
$\text{D.}$ $A$ 与 $C$ 不相似, $B$ 与 $C$ 不相似
设 $A, B$ 为随机事件, 若 $0 < P(A) < 1,0 < P(B) < 1$ ,则 $P(A \mid B)>P(A \mid \bar{B})$ 的充分必要条件是
$\text{A.}$ $P(B \mid A)>P(B \mid \bar{A})$
$\text{B.}$ $P(B \mid A) < P(B \mid \bar{A})$
$\text{C.}$ $P(\bar{B} \mid A)>P(B \mid \bar{A})$
$\text{D.}$ $P(\bar{B} \mid A) < P(B \mid \bar{A})$
设 $X_1, X_2 \ldots \ldots X_n(n \geq 2)$ 来自总体 $N(\mu, 1)$ 的简单随机样本,记 $\bar{X}=\frac{1}{n} \sum_{i=1}^n X_i$ ,则下列结论中不正确的是(
$\text{A.}$ $\sum_{i=1}^n\left(X_i-\mu\right)^2$ 服从 $\chi^2$ 分布
$\text{B.}$ $2\left(X_n-X_1\right)^2$ 服从 $\chi^2$ 分布
$\text{C.}$ $\sum_{i=1}^n\left(X_i-\bar{X}\right)^2$ 服从 $\chi^2$ 分布
$\text{D.}$ $n(\bar{X}-\mu)^2$ 服从 $\chi^2$ 分布
填空题 (共 6 题 ),请把答案直接填写在答题纸上
已知函数 $f(x)=\frac{1}{1+x^2}$ ,则 $f^{(3)}(0)=$
微分方程 $y^{\prime \prime}+2 y^{\prime}+3 y=0$ 的通解为 $y=$
若曲线积分 $\int_L \frac{x \mathrm{~d} x-a y \mathrm{~d} y}{x^2+y^2-1}$ 在区域
$$
D=\left\{(x, y) \mid x^2+y^2 < 1\right\}
$$
内与路径无关,则 $a=$
幂级数 $\sum_{n=1}^{\infty}(-1)^{n-1} n x^{n-1}$ 在区间 $(-1,1)$ 内的和函数 $S(x)=$
设矩阵 $A=\left(\begin{array}{lll}1 & 0 & 1 \\ 1 & 1 & 2 \\ 0 & 1 & 1\end{array}\right) , \alpha_1, \alpha_2, \alpha_3$ 为线性无关的 3 维列向量组,则向量组 $A \alpha_1, A \alpha_2, A \alpha_3$ 的秩为
设随机变量 $\boldsymbol{X}$ 的分布函数为
$$
F(x)=0.5 \Phi(x)+0.5 \Phi\left(\frac{x-4}{2}\right) ,
$$
其中 $\Phi(x)$ 为标准正态分布函数,则 $\boldsymbol{E}(\boldsymbol{X})=$
解答题 (共 9 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设函数 $f(u, v)$ 具有二阶连续偏导数, $y=f\left(e^x, \cos x\right)$ ,求 $\left.\frac{\mathrm{d} y}{\mathrm{~d} x}\right|_{x=0},\left.\frac{\mathrm{d}^2 y}{\mathrm{~d} x^2}\right|_{x=0}$.
求 $\lim _{n \rightarrow \infty} \sum_{k=1}^n \frac{k}{n^2} \ln \left(1+\frac{k}{n}\right)$.
已知函数 $y(x)$ 由方程 $x^3+y^3-3 x+3 y-2=0$ 确定,求 $y(x)$ 的极值.
设函数 $f(x)$ 在区间 $[0,1]$ 上具有二阶导数,且
$$
f(1)>0, \lim _{x \rightarrow 0^{+}} \frac{f(x)}{x} < 0 .
$$
证明:(1)方程 $f(x)=0$ 在区间 $(0,1)$ 内至少存在一个实根;
(2) 方程 $f(x) f^{\prime \prime}(x)+\left[f^{\prime}(x)\right]^2=0$ 在区间 $(0,1)$ 内至少存在两个不同实根.
设薄片型物体 $S$ 是圆锥面 $z=\sqrt{x^2+y^2}$ 被柱面 $z^2=2 x$割下的有限部分,其上任一点密度为
$$
\mu(x, y, z)=9 \sqrt{x^2+y^2+z^2} 。
$$
记圆锥与柱面的交线为 $C$ :
(1) 求 $C$ 在 $x O y$ 平面上的投影曲线的方程;
(2) 求 $S$ 的质量 $M$.
设 3 阶矩阵 $\boldsymbol{A}=\left(\alpha_1, \alpha_2, \alpha_3\right)$ 有 3 个不同的特征值,且 $\alpha_3=\alpha_1+2 \alpha_2$.
(1) 证明 $r(A)=2$ ;
(2) 如果 $\beta=\alpha_1+\alpha_2+\alpha_3$ ,求方程组 $\boldsymbol{A x}=\beta$ 的通解.
设二次型 $f\left(x_1, x_2, x_3\right)=2 x_1^2-x_2^2+a x_3^2+2 x_1 x_2$ $-8 x_1 x_3+2 x_2 x_3$ 在正交变换 $x=Q y$ 下的标准型为 $\lambda_1 y_1^2+\lambda_2 y_2^2$. 求 $a$ 的值及一个正交矩阵 $Q$.
设随机变量 $\boldsymbol{X}, \boldsymbol{Y}$ 相互独立,且 $\boldsymbol{X}$ 的概率分布为
$$
P\{X=0\}=P\{X=2\}=\frac{1}{2}
$$
$\boldsymbol{Y}$ 的概率概率密度为
$$
f(y)=\left\{\begin{array}{l}
2 y, 0 < y < 1, \\
0, \text { 其他. }
\end{array}\right.
$$
(1)求 $P\{\boldsymbol{Y} \leq \boldsymbol{E} Y\}$ ;
(2)求 $Z=X+Y$ 的概率密度.
某工程师为了解一台天平的精度,用该天平对一物体的质量做 $\boldsymbol{n}$ 次测量,该物体的质量 $\boldsymbol{\mu}$ 是已知的. 设 $\boldsymbol{n}$ 次测量结果 $X_1, X_2, \cdots, X_n$ 相互独立且均服从正态分布 $N\left(\mu, \sigma^2\right)$ ,该工程师记录的是 $\boldsymbol{n}$ 次测量的绝对误差
$$
Z_i=\left|X_i-\mu\right|(i=1,2, \cdots, n) .
$$
利用 $Z_1, Z_2, \cdots, Z_n$ 估计 $\sigma$.
(1) 求 $Z_1$ 的概率密度;
(2) 利用一阶矩求 $\sigma$ 的矩估计量;
(3) 求 $\sigma$ 的最大似然估计量.