设 $\triangle A B C$ 的内角 $A, B, C$ 的对边分别为 $a, b, c, \sin (B+C)=2 \sqrt{3} \sin ^2 \frac{A}{2}$
(1) 求角 $A$ 的大小;
(2) 若 $b=3, B C$ 边上的高为 $\frac{3 \sqrt{21}}{7}$ 。求 $\triangle A B C$ 的固长.

为了研究高三年级学生的性别和身高是否大于 $170 \mathrm{~cm}$ 的关联性, 随机调查了某中学部分高三年级的学生, 整理得到如下列联表 (单位: 人):

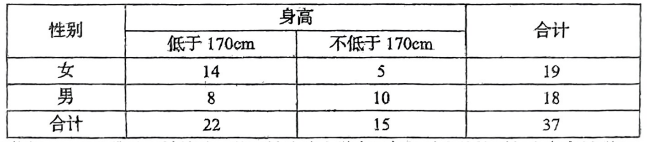
(1) 依据 $\alpha=0.1$ 的独立性检验, 能否认为该中学高三年级学生的性别与身高有关联?
(2) 从身高不低于 $170 \mathrm{~cm}$ 的 15 名学生中随机抽取三名学生, 设抽取的三名学生中女生人数为 $X$, 求 $X$ 的分布列及期望 $E(X)$.
(3) 若低于 $170 \mathrm{~cm}$ 的 8 名男生身高数据的平均数为 $\bar{x}=166.5$, 方差为 $s_1^2=9$, 不低于 $170 \mathrm{~cm}$的10 名男生身高数据的平均数为 $\bar{y}=180$, 方差为 $s_2{ }^2=18$. 请估计该中学男生身高数据的平均数和方差.

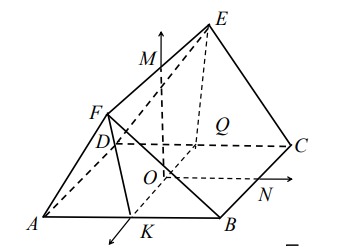
如图所示, 多面体 $A B C D E F$, 底面 $A B C D$ 是正方形, 点 $O$ 为底面的中心, 点 $M$ 为 $E F$的中点. 侧面 $A D E F$ 与 $B C E F$ 是全等的等腰梯形, $E F=4$, 其余棱长均为 2 .
(1) 证明: $M O \perp$ 平面 $A B C D$ ：
(2) 若点 $P$ 在梭 $C E$ 上, 直线 $B P$ 与平面 $A B M$ 所成角的正弦值为 $\frac{2 \sqrt{42}}{21}$, 求 $E P$.

在平面内, 若直线 $l$ 将多边形分为两部分, 多边形在 $l$ 两侧的顶点到直线 $l$ 的距离之和相等,则称 $l$ 为多边形的一条“等线”, 已知 $O$ 为坐标原点, 双曲线 $E: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 的左,右焦点分别为 $F_1, F_2, E$ 的离心率为 2 . 点 $P$ 为 $E$ 右支上一动点, 直线 $m$ 与曲线 $E$ 相切于点 $P$,且与 $E$ 的渐近线交于 $A, B$ 两点. 当 $P F_2 \perp x$ 轴时, 直线 $y=1$ 为 $\triangle P F_1 F_2$ 的等线.
(1) 求 $E$ 的方程;
(2) 若 $y=\sqrt{2} x$ 是四边形 $A F_1 B F_2$ 的等线, 求四边形 $A F_1 B F_2$ 的面积;
(3) 设 $\overrightarrow{O G}=\frac{1}{3} \overrightarrow{O P}$, 点 $G$ 的轨迹为曲线 $\Gamma$, 证明: $\Gamma$ 在点 $G$ 处的切线 $n$ 为 $\triangle A F_1 F_2$ 的等线.

已知 $O$ 为坐标原点, 曲线 $f(x)=a \ln x$ 在点 $P(1,0)$ 处的切线与曲线 $g(x)=\mathrm{e}^x+b$ 在点 $Q(0,1+b)$ 处的切线平行, 且两切线间的距离为 $\sqrt{2}$, 其中 $b \geq 0$.
(1) 求实数 $a, b$ 的值;
(2) 若点 $M, N$ 分别在曲线 $y=f(x), y=g(x)$ 上, 求 $\angle O N P$ 与 $\angle O M Q$ 之和的最大值;
(3) 若点 $A, B$ 在曲线 $y=f(x)$ 上, 点 $C, D$ 在曲线 $y=g(x)$ 上, 四边形 $A B C D$ 为正方形,其面积为 $S$, 证明: $S>2\left(\sqrt{\mathrm{e}}-\frac{1}{2}\right)^2$

附: $\ln 2 \approx 0.693$.