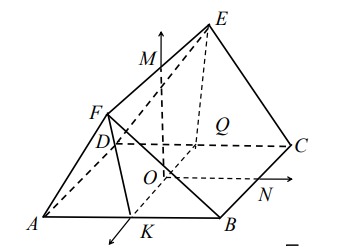
如图所示, 多面体 $A B C D E F$, 底面 $A B C D$ 是正方形, 点 $O$ 为底面的中心, 点 $M$ 为 $E F$的中点. 侧面 $A D E F$ 与 $B C E F$ 是全等的等腰梯形, $E F=4$, 其余棱长均为 2 .
(1) 证明: $M O \perp$ 平面 $A B C D$ ：
(2) 若点 $P$ 在梭 $C E$ 上, 直线 $B P$ 与平面 $A B M$ 所成角的正弦值为 $\frac{2 \sqrt{42}}{21}$, 求 $E P$.
$\text{A.}$
$\text{B.}$
$\text{C.}$
$\text{D.}$