某校举办乒乓球与羽毛球比赛，要求每个学生只能报名参加其中一项.从报名参加比赛的学生中随机选取男生、女生各75人进行调查,得到如下列联表:

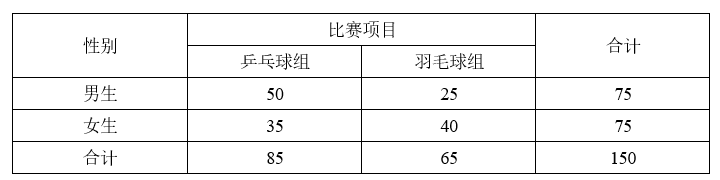
(1)根据表中数据,依据小概率值 $a=0.05$ 的独立性检验,分析该校学生选择乒乓球还是羽毛球是否与性别有关联.
(2)从调查的女生中,按组别采用比例分配的分层随机抽样的方法抽取15人.若从这15人中随机抽2人,记 X为抽到乒乓球组的学生人数,求X 的分布列及数学期望.

在 $\triangle A B C$ 中, 角 $A, B, C$ 所对的边分别为 $a, b, c$, 设向量 $\boldsymbol{m}=(2 \sin A, \sqrt{3} \sin A+\sqrt{3} \cos A)$, $\boldsymbol{n}=(\cos A, \cos A-\sin A), f(A)=\boldsymbol{m} \cdot \boldsymbol{n}, A \in\left[\frac{\pi}{6}, \frac{2 \pi}{3}\right]$.
(1) 求函数 $f(A)$ 的最大值;
(2)若 $f(A)=0, a=\sqrt{3}, \sin B+\sin C=\frac{\sqrt{6}}{2}$, 求 $\triangle A B C$ 的面积.

已知数列 $\left\{a_n\right\}$ 满足 $a_1=7, a_{n+1}= \begin{cases}a_n-3, & n \text { 为奇数, } \\ 2 a_n, & n \text { 为偶数. }\end{cases}$
(1) 写出 $a_2, a_3, a_4$;
(2) 证明: 数列 $\left\{a_{2 n-1}-6\right\}$ 为等比数列;
(3) 若 $b_n=a_{2 n}$, 求数列 $\left\{n \cdot\left(b_n-3\right)\right\}$ 的前 $n$ 项和 $S_n$.

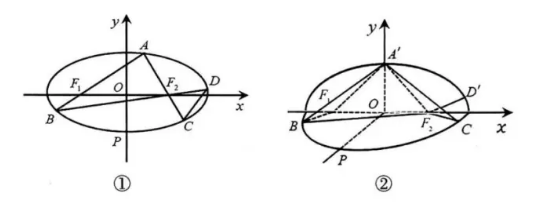
已知椭圆 $E: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的左、右焦点分别为 $F_1, F_2$, 离心率为 $\frac{\sqrt{2}}{2}$, 过点 $F_1$ 的动直线 $l$ 交 $E$ 于 $A, B$ 两点, 点 $A$ 在 $x$ 轴上方, 且 $l$ 不与 $x$ 轴垂直, $\triangle A B F_2$ 的周长为 $4 \sqrt{2}$, 直线 $A F_2$与 $E$ 交于另一点 $C$, 直线 $B F_2$ 与 $E$ 交于另一点 $D$, 点 $P$ 为椭圆 $E$ 的下顶点, 如图(1).
(1) 当点 $A$ 为椭圆 $E$ 的上顶点时, 将平面 $x O y$ 沿 $x$ 轴折叠如图 (2), 使平面 $A^{\prime} F_1 F_2 \perp$ 平面 $B F_1 F_2$, 求异面直线 $A^{\prime} C$ 与 $B F_1$ 所成角的余弦值;
(2) 若过 $F_2$ 作 $F_2 H \perp C D$, 垂足为 $H$.
(i) 证明: 直线 $C D$ 过定点;
(ii) 求 $|P H|$ 的最大值.

设集合 $M$ 是一个非空数集, 对任意 $x, y \in M$, 定义 $\rho(x, y)=|x-y|$, 称 $\rho$ 为集合 $M$ 的一个度量, 称集合 $M$ 为一个对于度量 $\rho$ 而言的度量空间, 该度量空间记为 $(M, \rho)$.

定义 1: 若 $f: M \rightarrow M$ 是度量空间 $(M, \rho)$ 上的一个函数, 且存在 $\alpha \in(0,1)$, 使得对任意 $x, y \in M$, 均有: $\rho(f(x), f(y)) \leqslant \alpha \rho(x, y)$, 则称 $f$ 是度量空间 $(M, \rho)$ 上的一个 “压缩函数”.

定义 2: 记无穷数列 $a_0, a_1, a_2, \cdots$ 为 $\left\{a_n\right\}_{n=0}^{+\infty}$, 若 $\left\{a_n\right\}_{n=0}^{+\infty}$ 是度量空间 $(M, \rho)$ 上的数列, 且对任意正实数 $\varepsilon>0$, 都存在一个正整数 $\mathbf{N}$, 使得对任意正整数 $m, n \geqslant \mathbf{N}$, 均有 $\rho\left(a_m, a_n\right) < \varepsilon$, 则称 $\left\{a_n\right\}_{n=0}^{+\infty}$ 是度量空间 $(M, \rho)$ 上的一个 “基本数列”.
(1) 设 $f(x)=\sin x+\frac{1}{2}$, 证明: $f$ 是度量空间 $\left(\left[\frac{1}{2}, 2\right], \rho\right)$ 上的一个 “压缩函数”;
(2) 已知 $f: \mathbf{R} \rightarrow \mathbf{R}$ 是度量空间 $(\mathbf{R}, \rho)$ 上的一个压缩函数, 且 $a_0 \in \mathbf{R}$, 定义 $a_{n+1}=f\left(a_n\right)$, $n=0,1,2, \cdots$, 证明: $\left\{a_n\right\}_{n=0}^{+\infty}$ 为度量空间 $(\mathbf{R}, \rho)$ 上的一个 “基本数列”.