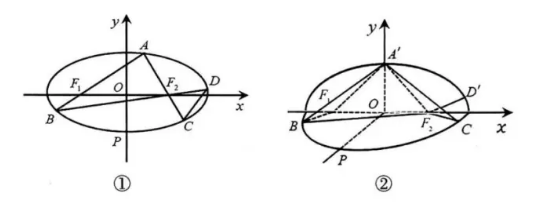
已知椭圆 $E: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的左、右焦点分别为 $F_1, F_2$, 离心率为 $\frac{\sqrt{2}}{2}$, 过点 $F_1$ 的动直线 $l$ 交 $E$ 于 $A, B$ 两点, 点 $A$ 在 $x$ 轴上方, 且 $l$ 不与 $x$ 轴垂直, $\triangle A B F_2$ 的周长为 $4 \sqrt{2}$, 直线 $A F_2$与 $E$ 交于另一点 $C$, 直线 $B F_2$ 与 $E$ 交于另一点 $D$, 点 $P$ 为椭圆 $E$ 的下顶点, 如图(1).
(1) 当点 $A$ 为椭圆 $E$ 的上顶点时, 将平面 $x O y$ 沿 $x$ 轴折叠如图 (2), 使平面 $A^{\prime} F_1 F_2 \perp$ 平面 $B F_1 F_2$, 求异面直线 $A^{\prime} C$ 与 $B F_1$ 所成角的余弦值;
(2) 若过 $F_2$ 作 $F_2 H \perp C D$, 垂足为 $H$.
(i) 证明: 直线 $C D$ 过定点;
(ii) 求 $|P H|$ 的最大值.