单选题 (共 4 题 ),每题只有一个选项正确
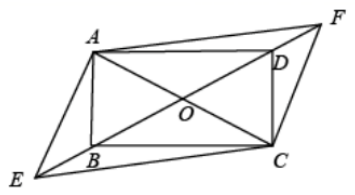
如图, 点 $E, F$ 在矩形 $A B C D$ 的对角线 $B D$ 所在的直线上, $B E=D F$, 则四边形 $A E C F$ 是
$\text{A.}$ 平行四边形
$\text{B.}$ 矩形
$\text{C.}$ 菱形
$\text{D.}$ 正方形
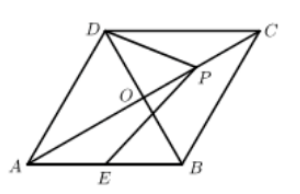
如图, 四边形 $A B C D$ 是菱形, 对角线 $A C, B D$ 相交于点 $O, A C=6 \sqrt{3}, B D=6$, 点 $P$ 是 $A C$ 上一动点,点 $E$ 是 $A B$ 的中点, 则 $P D+P E$ 的最小值为
$\text{A.}$ $3 \sqrt{3}$
$\text{B.}$ $6 \sqrt{3}$
$\text{C.}$ $3$
$\text{D.}$ $6 \sqrt{2}$
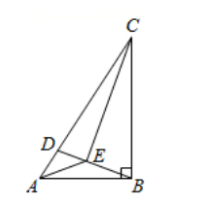
如图, 在 $\triangle A B C$ 中, $\angle A B C=90^{\circ}, A B=8$, $B C=12, D$ 为 $A C$ 边上的一个动点, 连接 $B D, E$ 为 $B D$ 上的一个动点, 连接 $A E, C E$, 当 $\angle A B D=\angle B C E$ 时, 线段 $A E$ 的最小值是
$\text{A.}$ 3
$\text{B.}$ 4
$\text{C.}$ 5
$\text{D.}$ 6
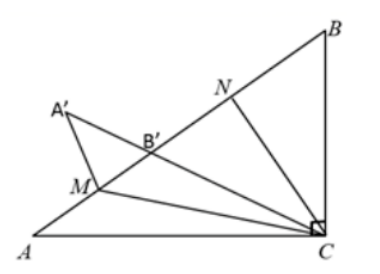
如图, 在 Rt $\triangle A B C$ 中, $\angle A C B=90^{\circ}, A C=8$, $B C=6$ 将边 $B C$ 沿 $C N$ 折叠, 使点 $\mathrm{B}$ 落在 $A B$ 上的点 $B^{\prime}$ 处, 再将边 $A C$沿 $C M$ 折叠, 使点 $\mathrm{A}$ 落在 $C B^{\prime}$ 的延长线上的点 $A^{\prime}$ 处, 两条折痕与斜边 $A B$ 分别交于点 $\mathrm{N} 、 \mathrm{M}$, 则线段 $A^{\prime} M$ 的长为
$\text{A.}$ $\frac{9}{5}$
$\text{B.}$ $\frac{8}{5}$
$\text{C.}$ $\frac{7}{5}$
$\text{D.}$ $\frac{6}{5}$