单选题 (共 8 题 ),每题只有一个选项正确
已知集合 $U=\{1,2,3,4,5\}, A=\{2,3\}, B=\{x \mid x=2 k, k \in \mathbf{Z}\}$, 则 $B \cap \complement_U A=$
$\text{A.}$ $\{4\}$
$\text{B.}$ $\{2,4\}$
$\text{C.}$ $\{1,2\}$
$\text{D.}$ $\{1,3,5\}$
复数 $\left(i-\frac{1}{i}\right)^3$ 的虚部为
$\text{A.}$ 8
$\text{B.}$ -8
$\text{C.}$ $8 \mathrm{i}$
$\text{D.}$ $-8 \mathrm{i}$
已知向量 $\boldsymbol{a}=(0,-2), \boldsymbol{b}=(1, t)$, 若向量 $\boldsymbol{b}$ 在向量 $\boldsymbol{a}$ 上的投影向量为 $-\frac{1}{2} \boldsymbol{a}$, 则 $\boldsymbol{a} \cdot \boldsymbol{b}=$
$\text{A.}$ 2
$\text{B.}$ $-\frac{5}{2}$
$\text{C.}$ -2
$\text{D.}$ $\frac{11}{2}$
在 $\triangle A B C$ 中, “ $C=\frac{\pi}{2}$ ” 是 “ $\sin ^2 A+\sin ^2 B=1$ ” 的
$\text{A.}$ 充分而不必要条件
$\text{B.}$ 必要而不充分条件
$\text{C.}$ 充分必要条件
$\text{D.}$ 既不充分也不必要条件
过点 $(0,-2)$ 与圆 $x^2+y^2-4 x-1=0$ 相切的两条直线的夹角为 $\alpha$, 则 $\cos \alpha=$
$\text{A.}$ $\frac{\sqrt{10}}{4}$
$\text{B.}$ $-\frac{1}{4}$
$\text{C.}$ $\frac{\sqrt{15}}{4}$
$\text{D.}$ $\frac{1}{4}$
$A, B, C, D, E$ 五人站成一排, 如果 $A, B$ 必须相邻, 那么排法种数为
$\text{A.}$ 24
$\text{B.}$ 180
$\text{C.}$ 48
$\text{D.}$ 60
若系列椭圆 $C_n: a_n x^2+y^2=1\left(0 < a_n < 1, n \in \mathbf{N}^*\right)$ 的离心率 $e_n=\left(\frac{1}{2}\right)^n$, 则 $a_n=$
$\text{A.}$ $1-\left(\frac{1}{4}\right)^n$
$\text{B.}$ $1-\left(\frac{1}{2}\right)^n$
$\text{C.}$ $\sqrt{1-\left(\frac{1}{2}\right)^n}$
$\text{D.}$ $\sqrt{1-\left(\frac{1}{4}\right)^n}$
已知等差数列 $\left\{a_n\right\}$ (公差不为 0 ) 和等差数列 $\left\{b_n\right\}$ 的前 $n$ 项和分别为 $S_n 、 T_n$, 如果关于 $x$ 的实系数方程 $1003 x^2-S_{1003} x+T_{1003}=0$ 有实数解, 那么以下 1003 个方程 $x^2-a_i x+b_i=0(i=1,2, \cdots, 1003)$ 中, 有实数解的方程至少有 ( ) 个
$\text{A.}$ 499
$\text{B.}$ 500
$\text{C.}$ 501
$\text{D.}$ 502
多选题 (共 3 题 ),每题有多个选项正确
已知一组数据: $12,31,24,33,22,35,45,25,16$, 若去掉 12 和 45 , 则剩下的数据与原数据相比,下列结论正确的是
$\text{A.}$ 中位数不变
$\text{B.}$ 平均数不变
$\text{C.}$ 方差不变
$\text{D.}$ 第 40 百分位数不变
双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$, 左、右顶点分别为 $A, B, O$ 为坐标原点, 如图, 已知动直线 $l$ 与双曲线 $C$ 左、右两支分别交于 $P, Q$ 两点, 与其两条渐近线分别交于 $R, S$ 两点, 则下列命题正确的是

$\text{A.}$ 存在直线 $l$, 使得 $A P / / O R$
$\text{B.}$ $l$ 在运动的过程中, 始终有 $|P R|=|S Q|$
$\text{C.}$ 若直线 $l$ 的方程为 $y=k x+2$, 存在 $k$, 使得 $S_{\triangle O R B}$ 取到最大值
$\text{D.}$ 若直线 $l$ 的方程为 $y=-\frac{\sqrt{2}}{2}(x-a), \overrightarrow{R S}=2 \overrightarrow{S B}$, 则双曲线 $C$ 的离心率为 $\sqrt{3}$
如图所示, 有一个棱长为 4 的正四面体 $P-A B C$ 容器, $D$ 是 $P B$ 的中点, $E$ 是 $C D$ 上的动点, 则下列说法正确的是
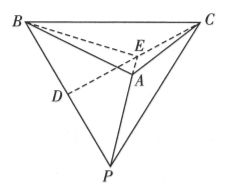
$\text{A.}$ 直线 $A E$ 与 $P B$ 所成的角为 $\frac{\pi}{2}$
$\text{B.}$ $\triangle A B E$ 的周长最小值为 $4+\sqrt{34}$
$\text{C.}$ 如果在这个容器中放人 1 个小球 (全部进人), 则小球半径的最大值为 $\frac{\sqrt{6}}{3}$
$\text{D.}$ 如果在这个容器中放人 4 个完全相同的小球 (全部进人), 则小球半径的最大值为 $\frac{2 \sqrt{6}-2}{5}$
填空题 (共 3 题 ),请把答案直接填写在答题纸上
已知函数 $f(x)=\ln (x+1)-\frac{a x}{x+1}$, 若 $f(x) \geqslant 0$ 恒成立, 则 $a=$
已知抛物线 $C: y^2=2 p x(p>0)$, 点 $P$ 为抛物线上的动点, 点 $A\left(4-\frac{p}{2}, 0\right)$ 与点 $P$ 的距离 $|A P|$ 的最小值为 2 , 则 $p=$
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
在 $\triangle A B C$ 中, $A, B, C$ 的对边分别为 $a, b, c$, 已知 $b=\sqrt{2}, c=4, a \cos C+b=0$.
(1) 求 $a$;
(2) 已知点 $D$ 在线段 $B C$ 上, 且 $\angle A D B=\frac{3 \pi}{4}$, 求 $A D$ 长.
甲、乙两人进行射击比赛, 每次比赛中, 甲、乙各射击一次, 甲、乙每次至少射中 8 环. 根据统计资料可知, 甲击中 8 环、 9 环、 10 环的概率分别为 0 . $7,0.2,0.1$, 乙击中 8 环、9 环、10 环的概率分别为 $0.6,0.2,0.2$, 且甲、乙两人射击相互独立.
(1) 在一场比赛中, 求乙击中的环数少于甲击中的环数的概率;
(2) 若独立进行三场比赛, 其中 X场比赛中甲击中的环数多于乙击中的环数,求 $\mathrm{X}$ 的分布列与数学期望.
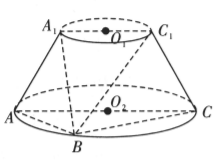
如图, 圆台 $O_1 O_2$ 的轴截面为等腰梯形 $A_1 A C C_1, A C=2 A A_1=2 A_1 C_1=4$, $B$ 为底面圆周上异于 $A, C$ 的点.
(1)在平面 $B C C_1$ 内, 过 $C_1$ 作一条直线与平面 $A_1 A B$ 平行, 并说明理由.
(2) 设平面 $A_1 A B \cap$ 平面 $C_1 C B=l, Q \in l, B C_1$ 与平面 $Q A C$ 所成角为 $\alpha$, 当四棱椎 $B-A_1 A C C_1$ 的体积最大时, 求 $\sin \alpha$ 的取值范围.
已知函数 $f(x)=\ln x-a x(x-1)$.
(1) 当 $a < 0$ 时,探究 $f^{\prime}(x)$ 零点的个数;
(2) 当 $a>0$ 时,证明: $f(x) \leqslant \frac{2+a}{\sqrt{a^2+8 a}-a}-\frac{3}{2}$.
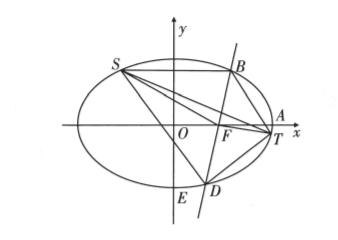
阿波罗尼斯是古希腊著名数学家, 他的主要研究成果集中在他的代表作《圆椎曲线》一书中. 阿波罗尼斯圆是他的研究成果之一, 指的是已知动点 $M$ 与两定点 $Q, P$ 的距离之比 $\frac{|M Q|}{|M P|}=\lambda(\lambda>0, \lambda \neq 1), \lambda$ 是一个常数, 那么动点 $M$ 的轨迹就是阿波罗尼斯圆, 圆心在直线 $P Q$ 上. 已知动点 $M$ 的轨迹是阿波罗尼斯圆, 其方程为 $x^2+y^2=4$, 定点分别为椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ $(a>b>0)$ 的右焦点 $F$ 与右顶点 $A$, 且椭圆 $C$ 的离心率为 $e=\frac{1}{2}$.
(1)求椭圆 $C$ 的标准方程;
(2) 如图, 过右焦点 $F$ 斜率为 $k(k>0)$ 的直线 $l$ 与椭圆 $C$ 相交于 $B, D$ (点 $B$ 在 $x$ 轴上方), 点 $S, T$ 是椭圆 $C$ 上异于 $B, D$ 的两点, $S F$ 平分 $\angle B S D, T F$ 平分 $\angle B T D$.
(1)求 $\frac{|B S|}{|D S|}$ 的取值范围;
(2) 将点 $S 、 F 、 T$ 看作一个阿波罗尼斯圆上的三点, 若 $\triangle S F T$ 外接圆的面积为 $\frac{81 \pi}{8}$,求直线 $l$ 的方程.