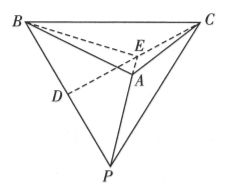
如图所示, 有一个棱长为 4 的正四面体 $P-A B C$ 容器, $D$ 是 $P B$ 的中点, $E$ 是 $C D$ 上的动点, 则下列说法正确的是

A. 直线 $A E$ 与 $P B$ 所成的角为 $\frac{\pi}{2}$
B. $\triangle A B E$ 的周长最小值为 $4+\sqrt{34}$
C. 如果在这个容器中放人 1 个小球 (全部进人), 则小球半径的最大值为 $\frac{\sqrt{6}}{3}$
D. 如果在这个容器中放人 4 个完全相同的小球 (全部进人), 则小球半径的最大值为 $\frac{2 \sqrt{6}-2}{5}$