解答题 (共 20 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知 $a+b+c+d=0, a b c d < 0$, 则 $\frac{|a|}{b+c+d}+\frac{|b|}{a+c+d}+\frac{|c|}{a+b+d}+\frac{|d|}{a+b+c}=$
已知, 在平行四边形 $A B C D$ 中, $E, F$ 分别是 $B C, C D$ 的中点 $A E=6, A F=3$ 且 $\angle E A F=60^{\circ}$, 则 $A B=$
阳光与水平面成 $60^{\circ}$ 角, 皮球在阳光下的影长为 $10 \sqrt{3} \mathrm{~cm}$, 则这个皮球的直径为 $\mathrm{cm}$ 。
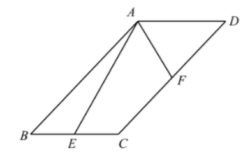
如图, $\triangle A B C, \triangle D E F$ 是等边三角形, 边长分别为 $3 、 2$, 求 $\triangle C D F$ 的内切圆的半径。
如图所示, 每个方格均为正方形, 线段 $A B$ 与 $C D$ 交于点 $P$, 求 $\sin \angle B P D$ 的值。

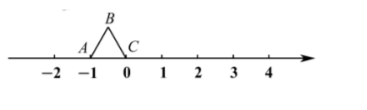
如图, 正三角形的边长为 1 , 点 $C$ 与原点重合, 现将正三角形向右翻转 2023 次, 求点 $B$ 在数轴上对应的数字。
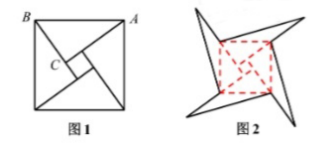
如图 1 是我国古代著名的 “赵爽弦图” 的示意图, 它由四个全等的直角三角形围成。若 $A C=6, B C=5$, 将四个直三形中边长为 6 的直角边分别向外延长一倍, 得到图 2 所示的 “数学风车, , 求这个风车的外围周长。
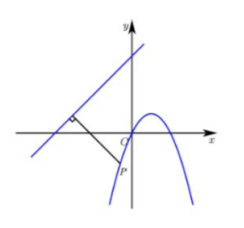
已知, 一次函数 $y_1=x+4, y_2=-x^2+2 x, P$ 为 $y_2$ 上一动点, 求 $P$ 到 $y_1$ 的距离的最小值。
已知整数 $x, y$ 满足 $x y=22-3 x+y$, 求 $x y$ 的最大值。
已知 $\frac{1}{x}-\frac{1}{y}=1$, 求 $\frac{4 x+5 x y-4 y}{x-3 x y-y}$ 的值。
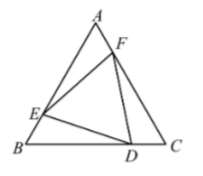
如图, 在矩形 $A B C D$ 中, 有正方形 $A E G F$, 正方形 $J H M I$, 正方形 $K L C M$, 问: 知道哪个正方形的面积可以得到两个阴影部分的周长之差。

已知任意一个大于 1 的正整数 $m$ 的三次幂均可以分裂成 $m$ 个连续奇数的和, 如 $2^3=3+5,3^3=7+9+11+\cdots$, 按照此规律, 若 $m^3$ 分裂后, 有一个奇数是 2023 , 求 $m$ 的值。
已知 $a, b, c, d, e$ 五个数的平均数为 $m$, 方差为 $g$, 求 $3 a+n, 3 b+n, 3 c+n, 3 d+n, 3 e+n$ 的平均数和方差。
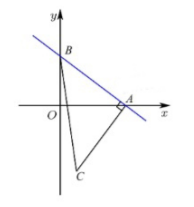
平面直角坐标系中, 已知直线 $A B: y=-\frac{3}{4} x+3$, 过 $A$ 作 $A C$ 垂直于 $A B$, 并使 $A C=A B$,求直线 $B C$ 的解析式。
球队两两比赛, 主场客场各一场, 共 42 场, 问有多少支队伍?
在平面直角坐标系中, 对于平面内任一点 $(a, b)$, 若规定以下两种变换: (1) $f(a, b)=(b, a)$,
如: $f(1,3)=(3,1)$; (2) $g(a, b)=(a,-b)$, 如: $g(1,3)=(1,-3)$; 那么 $f(g(5,-6))=$
我们用 $\min$ 表示两个数中的较小数, 如 $\min \{5,3\}=3$, 求 $\min \left\{-x^2-x, 2 x\right\}$ 的最大值。
已知关于 $x$ 的一元二次方程 $x^2-(n+2) x-2 n^2=0$ 的解为 $a_n, b_n$, 则 $\frac{2}{\left(a_1-2\right)\left(b_1-2\right)}+$ $\frac{2}{\left(a_2-2\right)\left(b_2-2\right)}+\cdots \frac{2}{\left(a_{2024}-2\right)\left(b_{2024}-2\right)}$ 的值。
假设队伍中共有 2 人现列队需要, 每 10 人中走出一个人, 当 $x$ 除以 10 的余数大于 5 时,则在余下的人中再走出一人, 则共走出多少人。
A. $\left[\frac{x}{10}\right]$
B. $\left[\frac{x+3}{10}\right]$
C. $\left[\frac{x+4}{10}\right]$
D. $\left[\frac{x+5}{10}\right]$
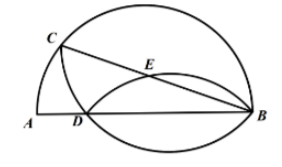
如图, $C$ 为半圆上一点, $A B$ 为直径, $\widehat{B C}$ 沿 $B C$ 翻折与 $A B$ 交于点 $D, \widehat{B D}$ 沿 $B D$ 翻折交 $B C$于 $E$, 若 $E$ 为 $B C$ 中点, 求 $\frac{A B}{B C}$ 的值。