解答题 (共 11 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设复数 $z=9+10 i(i$ 为虚数单位),若正整数 $n$ 满足 $\left|z^n\right| \leq 2023$ ,则 $n$ 的最大值为
若正实数 $a, b$ 满足 $a^{\lg b}=2, a^{\lg a} \cdot b^{\lg b}=5$ ,则 $(a b)^{\lg a b}$ 的值为
将一枚均匀的骰子独立投掷三次,所得的点数依次记为 $x, y, z$ ,则事件" $\mathrm{C}_7^x < \mathrm{C}_7^y < \mathrm{C}_7^z$ "发生的概率为
若平面上非零向量 $\vec{\alpha}, \vec{\beta}, \vec{\gamma}$ 满足 $\vec{\alpha} \perp \vec{\beta} , \vec{\beta} \cdot \vec{\gamma}=2|\vec{\alpha}|$ , $\vec{\gamma} \cdot \vec{\alpha}=3|\vec{\beta}|$ ,则 $|\vec{\gamma}|$ 的最小值为
方程 $\sin x=\cos 2 x$ 的最小的 20 个正实数解之和为
设 $a, b, c$ 为正数, $a < b$. 若 $a, b$ 为一元二次方程 $a x^2-b x+c=0$ 的两个根,且 $a, b, c$ 是一个三角形的三边长,则 $a+b-c$ 的取值范围是
平面直角坐标系 $x O y$ 中,已知圆 $\Omega$ 与 $x$ 轴、 $y$ 轴均相切,圆心在椭圆 $\Gamma: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 内,且 $\Omega$ 与 $\Gamma$有唯一的公共点 $(8,9)$. 则 $\Gamma$ 的焦距为
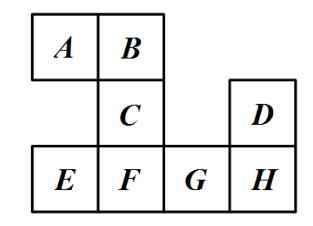
八张标有 $A, B, C, D, E, F, G, H$ 的正方形卡片构成下图.现逐一取走这些卡片,要求每次取走一张卡片时,该卡片与剩下的卡片中至多一张有公共边(例如可按 $D, A, B, E, C, F$, $G, H$ 的次序取走卡片,但不可按 $D, B, A, E, C, F, G, H$的次序取走卡片),则取走这八张卡片的不同次序的数目为
平面直角坐标系 $x O y$ 中,抛物线 $\Gamma: y^2=4 x , F$ 为 $\Gamma$ 的焦点. $A, B$ 为 $\Gamma$ 上的两个不重合的动点,使得线段 $A B$ 的一个三等分点 $P$ 位于线段 $O F$ 上 (含端点). 记 $Q$ 为线段 $A B$的另一个三等分点,求点 $Q$ 的轨迹方程.
已知三棱柱 $\Omega: A B C-A_1 B_1 C_1$ 的 9 条棱长均相等. 记底面 $A B C$ 所在平面为 $\alpha$. 若 $\Omega$ 的另外四个面 (即面 $A_1 B_1 C_1$, $\left.A B B_1 A_1, A C C_1 A_1, B C C_1 B_1\right)$ 在 $\alpha$ 上投影的面积从小到大重排后依次为 $2 \sqrt{3}, 3 \sqrt{3}, 4 \sqrt{3}, 5 \sqrt{3}$ ,求 $\Omega$ 的体积.
求出所有满足下面要求的不小于 1 的实数 $t$ : 对任意 $a, b \in[-1, t]$ ,总存在 $c, d \in[-1, t]$ ,使得 $(a+c)(b+d)=1$.