解答题 (共 11 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知质点位矢随时间变化的函数形式为 $r=4 t^2 \vec{i}+(3+2 t) \vec{j}$, 式中 $r$ 的 单位为 $m$, $t$ 的单位为 $s$ 。 求:
(1) 质点的轨道;
(2) 从 $t=0$ 到 $t=1$ 秒的位移;
(3) $t=0$ 和 $t=1$ 秒两时刻的速度。
已知质点位矢随时间变化的函数形式为 $\vec{r}=R(\cos \omega t \vec{i}+\sin \omega t \vec{j})$ 其中 $\omega$ 为常量. 求:
(1) 质点的轨道;
(2)速度和速率。
一弹性球直落在一斜面上,下落高度 $h=20 \mathrm{~cm}$, 斜面对水平的倾角$\theta=30^{\circ}$ ,问它第二次碰到斜面的位置距原来的下落点多远(假设小球碰斜面前后速度数值相等, 碰撞时入射角等于反射角)
质量为 $2 \mathrm{~kg}$ 的质点在 $\mathrm{xy}$ 平面上运动, 受到外力 $\vec{F}=4 \vec{i}-24 t^2 \vec{j}$ 的作用, $t=0$ 时, 它的初速度为 $\vec{v}_0=3 \vec{i}+4 \vec{j}$, 求 $t=1 \mathrm{~s}$ 时质点的速度及受到的 法向力 $\vec{F}_n$
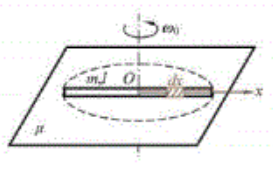
如图所示, 一均匀细杆长为 $l$, 质量为 $m$, 平放在摩擦系数为 $\mu$ 的水平桌面上, 设开始时杆以角速度 $\omega_0$ 绕过中心 0 且垂直与桌面的轴 转动, 试求: (1) 作用于杆的摩擦力矩; (2) 经过多长时间杆才会 停止转动。
质量分别为 $m_1$ 和 $m_2$ 的两滑块 $A$ 和 $B$ 通过一轻弹簧水平连结后 置于水平桌面上, 滑块与桌面间的摩擦系数均为 $\mu$, 系统在水平拉 力 $F$ 作用下匀速运动, 如图所示. 如突然撤消拉力, 则刚撤消后瞬 间, 二者的加速度 $a_A$ 和 $a_B$ 分别为多少?

原长为 $0.5 \mathrm{~m}$ 的弹簧, 上端固定, 下端挂一质量为 $0.1 \mathrm{~kg}$ 的物体, 当 物体静止时, 弹簧长为 $0.6 \mathrm{~m}$. 现将物体上推, 使弹簧缩回到原长, 然 后放手, 以放手时开始计时, 取坚直向下为正向, 写出振动式。( $\mathrm{g}$ 取 9.8)
两个同方向, 同频率的简谐振动, 其合振动的振幅为 $20 \mathrm{~cm}$, 与 第一个振动的位相差为 $\frac{\pi}{6}$ 。若第一个振动的振幅为 $10 \sqrt{3} \mathrm{~cm}$ 。则 (1) 第二个振动的振幅为多少? (2) 两简谐振动的位相差为多少?
一声源的频率为 $1080 \mathrm{~Hz}$, 相对于地以 $30 \mathrm{~m} / \mathrm{s}$ 的速度向右运动, 在其右方有一反射面相对于地以 $65 \mathrm{~m} / \mathrm{s}$ 的速率向左运动, 设空气中 的声速为 $331 \mathrm{~m} / \mathrm{s}$, 求:
(1) 声源在空气中发出声音的波长;
(2)每秒钟到达反射面的波数;
(3) 反射波的波速;
(4) 反射波的波长。
已知某种理想气体, 其分子方均根率为 $400 \mathrm{~m} / \mathrm{s}$, 当其压强为 1 atm 时, 求气体的密度。
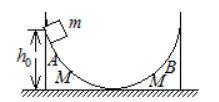
两个形状完全相同、质量都为 $M$ 的弧形导轨 $A$ 和 $B$, 相向地放在地板上, 今 有一质量为 $m$ 的小物体, 从静止状态由 $A$ 的顶端下滑, $A$ 顶端的高度为 $h_0$, 所有接触面均 光滑。试求小物体在 $B$ 轨上上升的最大高度 (设 $A 、 B$ 导轨与地面相切)。