单选题 （共 12 题 ），每题只有一个选项正确
$-2008$ 的相反数是
$\text{A.}$ $2008$
$\text{B.}$ $-2008$
$\text{C.}$ $\frac{1}{2008}$
$\text{D.}$ $-\frac{1}{2008}$
以 “和谐之旅” 为主题的北京奥运会火炬接力,传递总里程约为 137000 千米,这个数据用 科学记数法可表示为
$\text{A.}$ $13.7 \times 10^3$ 千米
$\text{B.}$ $13.7 \times 10^4$ 千米
$\text{C.}$ $1.37 \times 10^5$ 千米
$\text{D.}$ $1.37 \times 10^6$ 千米
在算式 $4-| -3 \square 5 | $ 中的口所在位置, 填入下列哪种运算符号, 计算出来的值最小
$\text{A.}$ $ + $
$\text{B.}$ $ - $
$\text{C.}$ $ \times $
$\text{D.}$ $ \div$
一几何体的三视图如右,这个几何体是
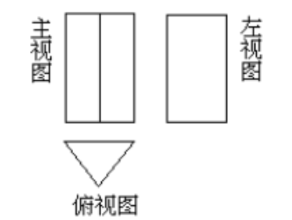
$\text{A.}$ 圆椎
$\text{B.}$ 圆柱
$\text{C.}$ 三棱椎
$\text{D.}$ 三棱柱
我市 5 月某一周每天的最高气温统计如下:
则这组数据 (最高气温) 的众数与中位数分别是
$\text{A.}$ 29,30
$\text{B.}$ 30,29
$\text{C.}$ 30,30
$\text{D.}$ 30,31
下列运算中正确的是
$\text{A.}$ $x^3 \cdot y^3=x^6$
$\text{B.}$ $\left(m^2\right)^3=m^5$
$\text{C.}$ $2 x^{-2}=\frac{1}{2 x^2}$
$\text{D.}$ $(-a)^6 \div(-a)^3=-a^3$
如图, $a // b, M 、 N$ 分别在 $a 、 b$ 上, $P$ 为两平行线间一点, 那么 $\angle 1+\angle 2+\angle 3=$
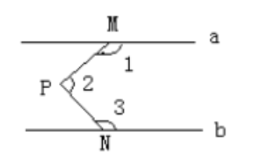
$\text{A.}$ $180^{\circ}$
$\text{B.}$ $270^{\circ}$
$\text{C.}$ $360^{\circ}$
$\text{D.}$ $540^{\circ}$
下列曲线中, 表示 $y$不是$x$的函数是
$\text{A.}$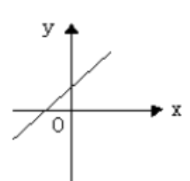 
$\text{B.}$ 
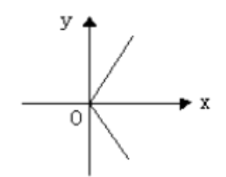$\text{C.}$ 
$\text{D.}$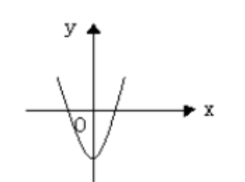 
下列图形中,既是轴对称图形又是中心对称图形的是
$\text{A.}$ 菱形
$\text{B.}$ 梯形
$\text{C.}$ 正三角形
$\text{D.}$ 正五边形
把抛物线 $y=-x^2$ 向左平移 1 个单位, 然后向上平移 3 个单位, 则平移后抛物线的解析式 为
$\text{A.}$ $y=-(x-1)^2-3$
$\text{B.}$ $y=-(x+1)^2-3$
$\text{C.}$ $y=-(x-1)^2+3$
$\text{D.}$ $y=-(x+1)^2+3$
$ Rt \triangle A B C$ 中, $\angle C=90^{\circ}, \mathrm{AC}=8, \mathrm{BC}=6$, 两等圆 $\odot A 、 \odot B$ 外切, 那么图中两个扇形（即阴 影部分）的面积之和为
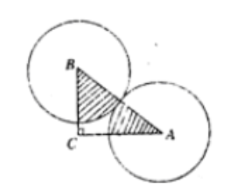
$\text{A.}$ $\frac{25}{4} \pi$
$\text{B.}$ $\frac{25}{8} \pi$
$\text{C.}$ $\frac{25}{16} \pi$
$\text{D.}$ $\frac{25}{32} \pi$
一个质点在第一象限及 $\mathrm{x}$ 轴、 $\mathrm{y}$ 轴上运动, 在第一秒钟, 它从原点运动到 $(0,1)$, 然后接着 按图中箭头所示方向运动 [即 $(0,0) \rightarrow(0,1) \rightarrow(1,1) \rightarrow(1,0) \rightarrow \cdots]$, 且每秒移动一个单位, 那么第 35 秒时质点所在位置的坐标是
$\text{A.}$ $(4,0)$
$\text{B.}$ $(5,0)$
$\text{C.}$ $(0,5)$
$\text{D.}$ $(5,5)$
填空题 （共 6 题 ），请把答案直接填写在答题纸上
反比例函数 $y=\frac{k}{x}$ 的图象过点 $(2,-3)$, 则 $\mathrm{k}=$
某校九年级一班数学单元测验全班所有学生成绩的频数分布直方图如图所示（满分 100 分, 学生成绩取整数), 则成绩在 $90.5-95.5$ 这一分数段的频率是
如图, $\mathrm{AB}=\mathrm{AC}, \angle B A C=120^{\circ}, \mathrm{AB}$ 的垂直平分线交 $\mathrm{BC}$ 于点 $\mathrm{D}$, 那么 $\angle A D C=$
不等式组 $\left\{\begin{array}{l}x+8 \prec 4 x-1 \\ \frac{1}{2} x \geq 4-\frac{3}{2} x\end{array}\right.$ 的解集是
在实数范围内定义运算"★" ，其规则为： $a★b=a^2-b^2$ ，则方程 (4★3)★x=13 的解为 $x=$
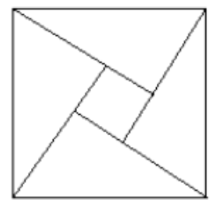
四个全等的直角三角形围成一个大正方形,中间空出的部分是一个小正方形, 这样就组成 了一个 “赵爽弦图” (如图)。如果小正方形面积为 1 , 大正方形面积为 25 , 直角三角形中较小 锐角为 $\theta$, 那么 $\sin \theta=$
解答题 （共 7 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
请你先将式子 $\frac{2008 a}{a^2-2 a+1} \div\left(1+\frac{1}{a-1}\right)$ 化简, 然后从 $1,2,3$ 中选择一个数作为 $a$ 的值代入其中求值。
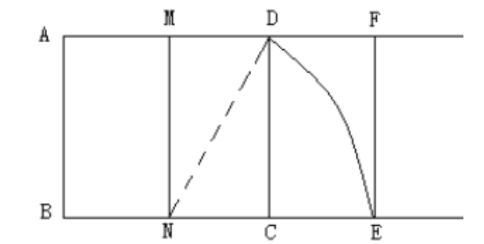
宽与长的比是 $\frac{\sqrt{5}-1}{2}$ 的矩形叫黄金矩形, 心理学测试表明, 黄金矩形令人赏心悦 目, 它给我们以协调、匀称的美感。现将同学们在教学活动中, 折叠黄金矩形的方法归纳出以 下作图步骤 (如图所示):
第一步：作一个任意正方形 $\mathrm{ABCD}$
第二步：分别取 $A D 、 B C$ 的中点 $M 、 N$,连接 $M N$ 。
第三步: 以 $\mathrm{N}$ 为圆心, $\mathrm{ND}$ 长为半径画弧, 交 $\mathrm{BC}$ 的延长线于 $\mathrm{E}$ 。
第四步：过 $\mathrm{E}$ 作 $E F \perp A D$ 交 $\mathrm{AD}$ 的延长线于 $\mathrm{F}$,
请你根据以上作法,证明矩形 $\mathrm{DCEF}$ 为黄金矩形, (可取 $\mathrm{AB}=2$ )。
2021 年北京奥运会吉祥物是 “贝贝贝、“晶晶”、“欢欢”、“迎迎”、“妮妮”, 现 将 5 张分别写有这五个吉祥物名称的卡片（卡片的形状、大小一样, 质地相同, 如图所示）放 入一个不透明的盒子内搅匀。
（1）小虹从盒子中任取一张卡片,取到 “欢欢” 的概率是多少?
(2) 小虹从盒子中先随机取出一张卡片 (不放回盒子), 然后再从盒子中取出第二张卡片, 请 你用列表法或树形图法表示出小虹两次取到卡片的所有可能情况, 并求出两次取到的卡片恰 好是 “贝贝”、“晶晶” (不考虑先后顺序) 的概率。
已知关于 $\mathrm{x}$ 的一元二次方程 $x^2+(2 m-1) x+m^2=0$ 有两个实数根 $x_1$ 和 $x_2$ 。
(1) 求实数 $\mathrm{m}$ 的取值范围。
(2) 当 $x_1^2-x_2^2=0$ 时, 求 $m$ 的值。
(友情提示: 若 $x_1 、 x_2$ 是一元二次方程 $a x^2+b x+c=0(a \neq 0)$ 两根, 则有 $x_1+x_2=-\frac{b}{a}$,
$$
( x_1 \cdot x_2=\frac{c}{a} )
$$
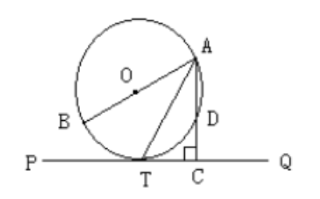
如图, $\mathrm{AB}$ 为 $\odot O$ 的直径, $\mathrm{PQ}$ 切 $\odot O$ 于 $\mathrm{T}, A C \perp P Q$ 于 $\mathrm{C}$, 交 $\odot O$ 于 $\mathrm{D}$ 。
（1）求证: $\mathrm{AT}$ 平分 $\angle B A C$ 。
(2) 若 $\mathrm{AD}=2, T C=\sqrt{3}$, 求 $\odot O$ 的半径。
根据公司实际情况,对本公司职工实行内部医疗公积金制度,公司规定：
(一) 每位职工在年初需缴纳医疗公积金 $\mathrm{m}$ 元。
（二）职工个人当年治病花费的医疗费年底按表 1 的办法分段处理:
表 1
设一职工当年治病花费的医疗费为 $\mathrm{x}$ 元, 他个人实际承担的费用（包括医疗费个人承担的部 分和缴纳的医疗公积金 $\mathrm{m}$ 元) 为 $\mathrm{y}$ 元
(1) 由表 1 可知,当 $0 \leq x \leq 150$ 时, $y=x+m$ 。那么, 当 $150 \prec x \leq 10000$ 时, $\mathrm{y}=$
(用含 $m 、 n 、 x$ 的方式表示)
(2) 该公司职工小陈和大李 2007 年治病花费的医疗费和他们个人实际承担的费用如表 2 :
请根据表 2 中的信息,求 $\mathrm{m} 、 \mathrm{n}$ 的值,并求出当 $150 \prec x \leq 10000$ 时, $\mathrm{y}$ 关于 $\mathrm{x}$ 函数解析式。
(3) 该公司职工个人一年因病实际承担费用最多只需要多少元? (直接写出结果)
锐角 $\triangle A B C$ 中, $\mathrm{BC}=6, S_{\triangle A B C}=12$, 两动点 $\mathrm{M}, \mathrm{N}$ 分别在边 $\mathrm{AB} 、 \mathrm{AC}$ 上滑动, 且
$M N // B C$, 以 $\mathrm{MN}$ 为边向下作正方形 $M P Q N$, 设其边长为 $\mathrm{x}$, 正方形 $M P Q N$ 与 $\triangle A B C$ 公共部分的
面积为 $\mathrm{y}(y \succ 0)$
(1) $\triangle A B C$ 中边 $\mathrm{BC}$ 上高 $\mathrm{AD}=$
(2) 当 $x=$ 时,PQ 恰好落在边 $\mathrm{BC}$ 上（如图 1)。
(3) 当 $\mathrm{PQ}$ 在 $\triangle A B C$ 外部时 (如图 2), 求 $\mathrm{y}$ 关于 $\mathrm{x}$ 的函数关系式 (注名 $\mathrm{x}$ 的取值范围), 并求出 $\mathrm{x}$ 为何值时 $\mathrm{y}$ 最大, 最大值是多少?