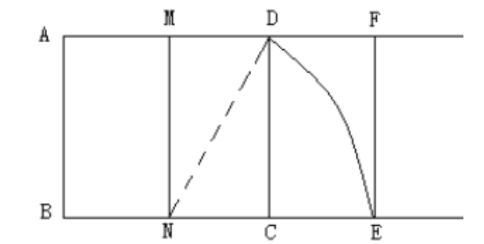
宽与长的比是 $\frac{\sqrt{5}-1}{2}$ 的矩形叫黄金矩形, 心理学测试表明, 黄金矩形令人赏心悦 目, 它给我们以协调、匀称的美感。现将同学们在教学活动中, 折叠黄金矩形的方法归纳出以 下作图步骤 (如图所示):
第一步：作一个任意正方形 $\mathrm{ABCD}$
第二步：分别取 $A D 、 B C$ 的中点 $M 、 N$,连接 $M N$ 。
第三步: 以 $\mathrm{N}$ 为圆心, $\mathrm{ND}$ 长为半径画弧, 交 $\mathrm{BC}$ 的延长线于 $\mathrm{E}$ 。
第四步：过 $\mathrm{E}$ 作 $E F \perp A D$ 交 $\mathrm{AD}$ 的延长线于 $\mathrm{F}$,
请你根据以上作法,证明矩形 $\mathrm{DCEF}$ 为黄金矩形, (可取 $\mathrm{AB}=2$ )。