单选题 (共 8 题 ),每题只有一个选项正确
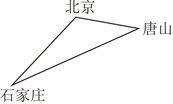
北京、石家庄、唐山三地所在的位置如图所示,若想建立一个货物中转仓,使其到这三地的距离相等,则中转仓的位置应选在
$\text{A.}$ 三边垂直平分线的交点处
$\text{B.}$ 三边中线的交点处
$\text{C.}$ 三条角平分线的交点处
$\text{D.}$ 三边上高的交点处
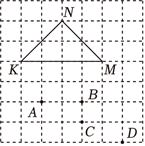
如图,在点 $A, B, C, D$ 中选一个点;与点 $M, N$ 为顶点构成一个三角形,其面积等于 $\triangle K M N$ 的面积,这个点为( )
$\text{A.}$ 点 $A$
$\text{B.}$ 点 $B$
$\text{C.}$ 点 $C$
$\text{D.}$ 点 $D$
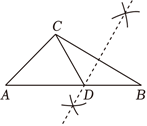
如图,在 $\triangle A B C$ 中,$\angle A=45^{\circ}, \angle B=30^{\circ}$ .用直尺和圆规在边 $A B$ 上确定一点 $D . \angle A C D$ 的大小为( )
$\text{A.}$ $60^{\circ}$
$\text{B.}$ $65^{\circ}$
$\text{C.}$ $70^{\circ}$
$\text{D.}$ $75^{\circ}$
在 $\triangle A B C$ 中,$A B=2, A C=2 \sqrt{3}, \angle C=30^{\circ}$ ,则线段 $B C$ 的长为
$\text{A.}$ 4
$\text{B.}$ $2 \sqrt{2}$
$\text{C.}$ 4 或 $2 \sqrt{2}$
$\text{D.}$ 2 或 4
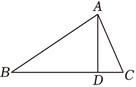
如图,$\triangle A B C$ 中,$\angle C=90^{\circ}, D$ 是 $B C$ 边上的一点,$\angle 1=\angle 2, B C=10, B D=6$ ,则点 $D$ 到 $A B$ 的距离为
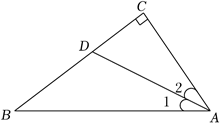
$\text{A.}$ 4
$\text{B.}$ 6
$\text{C.}$ 8
$\text{D.}$ 10
一个三角形的两边长分别为 3 cm 和 4 cm ,则第三边的长可能是( )
$\text{A.}$ 1 cm
$\text{B.}$ 2 cm
$\text{C.}$ 7 cm
$\text{D.}$ 8 cm
如图,$m / / n, \triangle A B C$ 的顶点 $C$ 在直线 $m$ 上,若 $A B=A C, \angle A=40^{\circ}, \angle 1=20^{\circ}$ ,则 $\angle$ 2 的度数为
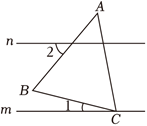
$\text{A.}$ $50^{\circ}$
$\text{B.}$ $40^{\circ}$
$\text{C.}$ $45^{\circ}$
$\text{D.}$ $60^{\circ}$
直角三角形中,两锐角的角平分线所夹的钝角的度数是
$\text{A.}$ $120^{\circ}$
$\text{B.}$ $135^{\circ}$
$\text{C.}$ $150^{\circ}$
$\text{D.}$ $160^{\circ}$
填空题 (共 9 题 ),请把答案直接填写在答题纸上
如图,Rt $\triangle A B C, \angle A C B=90^{\circ}, A C=4, A B=5$ ,点 $M 、 D 、 E$ 分别位于 $A B 、 A C 、 B C$ 上, $M D \perp M E$ ,且 $M E=2 M D$ ,则 $B M=$ $\qquad$ .
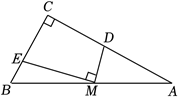
如图,$A, B, C, D, E$ 五个顶点均在小正方形组成的网格的格点上.若 $E F \perp B D$ 于点 $F$ ,且 $E F=1$ ,则 $D E$ 的长为 $\qquad$ .
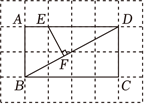
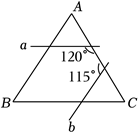
如图为两直线 $a, b$ 与 $\triangle A B C$ 相交的情形,其中 $a, b$ 分别与 $B C, A B$ 平行.根据图中标示的角度,回答下列问题.
(1)$a$ 与 $b$ 所夹锐角的度数为 $\qquad$ ;
(2)$\angle B$ 的度数为 $\qquad$ ${ }^{\circ}$ .
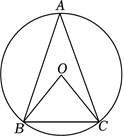
如图,在 $\odot O$ 中,弦 $A B=A C, \angle A B O=20^{\circ}$ ,则 $\angle B O C$ 的度数为
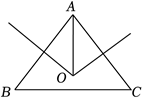
如图,在 $\triangle A B C$ 中,$A B=A C=5, B C=6$ ,线段 $A B, A C$ 的垂直平分线交于点 $O$ ,则 $O A$ 的长度为 $\qquad$ .
如图,将一副三角尺摆放在一起,含 $45^{\circ}$ 角的三角尺的斜边与含 $30^{\circ}$ 角的三角尺的较长直角边恰好重合,作 $A E \perp C D$ 于点 $E$ ,连结 $B E$ ,则 $\angle A B E$ 的大小为
如图,在 $\triangle A B C$ 中,$\angle C=2 \angle B, A D \perp B C$ ,垂足为 $D, A B=5, A D=3$ ,则 $A C=$ $\qquad$ .
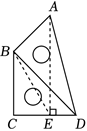
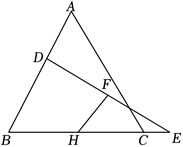
如图,$\triangle A B C$ 是等边三角形,$A B=10, D$ 为 $A B$ 上一点,$D B=\frac{3}{5} A B, D E \perp A B$ 与 $B C$ 的延长线相交于点 $E, F$ 为 $D E$ 的中点,$H$ 为 $B C$ 的中点,连接 $F H$ .则 $F H$ 的长为 $\qquad$ .
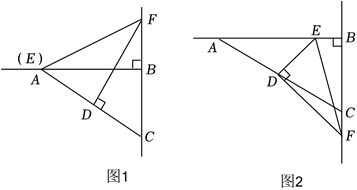
如图,Rt $\triangle A B C$ 中,$\angle A B C=90^{\circ}, D$ 为 $A C$ 中点,点 $F$ 在直线 $B C$ 上(点 $F$ 不与点 $B, C$重合),连接 $D F$ ,过点 $D$ 作 $D E \perp D F$ 交直线 $A B$ 于点 $E$ ,连接 $E F$ .
(1)如图 1,当点 $E$ 与点 $A$ 重合时,请直接写出线段 $E F$ 与 $C F$ 的数量关系 $\qquad$ ;
(2)如图 2,当点 $E$ 不与点 $A$ 重合时,请猜想 $A E 、 C F 、 E F$ 的数量关系 $\qquad$小明是这样做的,延长 $F D$ 到 $H$ ,使 $F D=D H$ ,连接 $H A$ 后可证 $\triangle F D C \cong \triangle H D A$ ,可得 $A H=C F$ ,再连接 $H E$ ,再利用 $\triangle E D H \cong \triangle E D F$ ,可得 $H E=E F$ ,利用 $A H / / C F$ 导出 $\angle H A E =90^{\circ}$ ,在 Rt $\triangle H A E$ 中利用勾股定理就可以导出 $A E 、 C F 、 E F$ 之间的关系了,你学明白了吗,现在请把小明的证明过程完整的写出来.
证明题 (共 3 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
如图,在 $\triangle A B C$ 中,$A B=A C, \angle B A C=2 \alpha\left(45^{\circ} < \alpha < 90^{\circ}\right) D$ 是 $B C$ 的中点,$E$ 是 $B D$ 的中点,连接 $A E$ .将射线 $A E$ 绕点 $A$ 逆时针旋转 $\alpha$ 得到射线 $A M$ ,过点 $E$ 作 $E F \perp A E$ 交射线 $A M$ 于点 $F$ .
(1)
① 依题意补全图形;
② 求证:$\angle B=\angle A F E$ ;
(2)连接 $C F, D F$ ,用等式表示线段 $C F, D F$ 之间的数量关系,并证明.
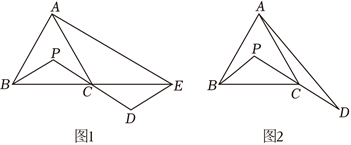
等边 $\triangle A B C$ 的边长为 $2, P$ 为 $\triangle A B C$ 内一点,连接 $B P, P C$ ,延长 $P C$ 到点 $D$ ,使 $C D=P C$ .
(1)如图 1,延长 $B C$ 到点 $E$ ,使 $C E=B C$ ,连接 $A E, D E$ .
① 求证:$B P / / D E$ ;
② $\angle B A E=$ $\qquad$ ;若 $B P \perp A C$ ,求 $\angle A E D$ 的度数;
(2)如图 2,连接 $A D$ ,若 $B P \perp A D, B P=1$ ,求 $A D$ 的长.
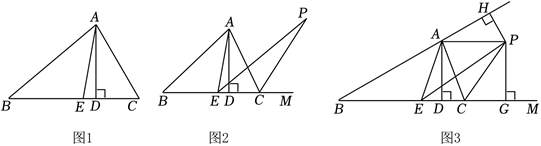
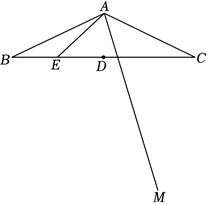
已知 $\triangle A B C$ 中,$A D$ 是 $B C$ 边上的高,$A E$ 是 $\triangle A B C$ 的角平分线.
(1)如图 1,若 $\angle B=40^{\circ}, \angle C=60^{\circ}$ ,求 $\angle E A D$ 的度数;
(2)如图 2,PE、PC 分别平分 $\angle A E C$ 和 $\triangle A C B$ 的外角 $\angle A C M$ ,请直接写出 $\angle P$ 与 $\angle B A C$的数量关系;
(3)如图 3,在(2)的条件下,连接 $P A$ ,过 $P$ 作 $P G \perp B C$ 交 $B C$ 延长线于 $G$ ,若 $\angle E A D =\angle C A D=2 \alpha$ ,且 $\angle \mathrm{B}+\angle \mathrm{CPE}=\frac{10}{7} \angle \mathrm{CPG}, P H \perp A B$ 交 $B A$ 的延长线于 $H$ ,求 $\angle E P H$ 的度数.