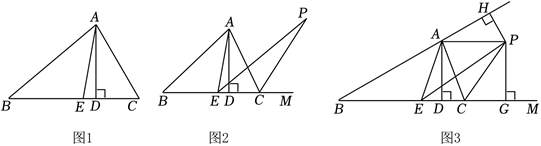
已知 $\triangle A B C$ 中，$A D$ 是 $B C$ 边上的高，$A E$ 是 $\triangle A B C$ 的角平分线．
（1）如图 1，若 $\angle B=40^{\circ}, \angle C=60^{\circ}$ ，求 $\angle E A D$ 的度数；
（2）如图 2，PE、PC 分别平分 $\angle A E C$ 和 $\triangle A C B$ 的外角 $\angle A C M$ ，请直接写出 $\angle P$ 与 $\angle B A C$的数量关系；
（3）如图 3，在（2）的条件下，连接 $P A$ ，过 $P$ 作 $P G \perp B C$ 交 $B C$ 延长线于 $G$ ，若 $\angle E A D =\angle C A D=2 \alpha$ ，且 $\angle \mathrm{B}+\angle \mathrm{CPE}=\frac{10}{7} \angle \mathrm{CPG}, P H \perp A B$ 交 $B A$ 的延长线于 $H$ ，求 $\angle E P H$ 的度数．