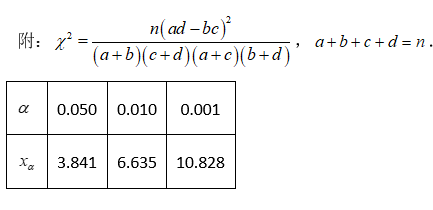单选题 (共 9 题 ),每题只有一个选项正确
调查某种花萼长度和花瓣长度,所得数据如图所示,其中相关系数 $r=0.8245$ ,下列说法正确的是
$\text{A.}$ 花瓣长度和花萼长度没有相关性
$\text{B.}$ 花瓣长度和花萼长度呈现负相关
$\text{C.}$ 花瓣长度和花萼长度呈现正相关
$\text{D.}$ 若从样本中抽取一部分,则这部分的相关系数一定是 0.8245
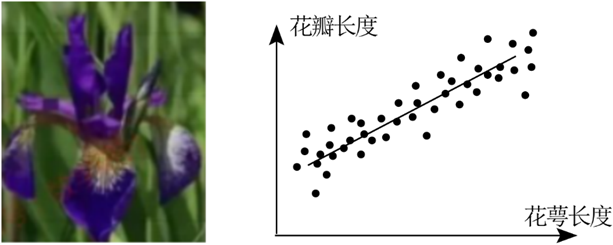
根据所示的散点图,下列说法正确的是( )
$\text{A.}$ 身高越大,体重越大
$\text{B.}$ 身高越大,体重越小
$\text{C.}$ 身高和体重成正相关
$\text{D.}$ 身高和体重成负相关
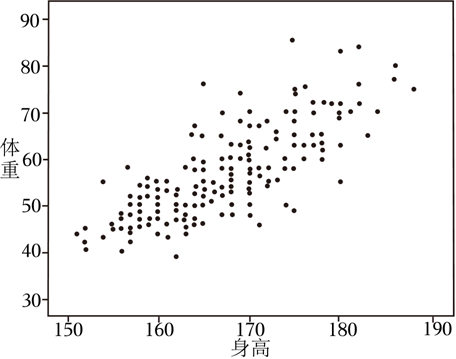
为研究变量x,y的相关关系,收集得到下面五个样本点(x,y):
若由最小二乘法求得 $y$ 关于 $x$ 的回归直线方程为 $\hat{y}=-1.8 x+\hat{a}$ ,则据此计算残差为 0 的样本点是( )
$\text{A.}$ $(5,9)$
$\text{B.}$ $(6.5,8)$
$\text{C.}$ $(7,6)$
$\text{D.}$ $(8,4)$
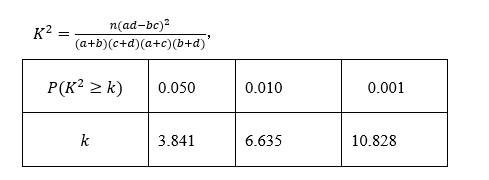
根据分类变量 $x$ 与 $y$ 的成对样本数据,计算得到 $\chi^2=6.147$ .依据 $\alpha=0.01$ 的独立性检验 $\left(P\left(\chi^2\right) \geqslant 6.635=0.01\right)$ ,结论为( )
$\text{A.}$ 变量 $x$ 与 $y$ 不独立
$\text{B.}$ 变量 $x$ 与 $y$ 不独立,这个结论犯错误的概率不超过 0.01
$\text{C.}$ 变量 $x$ 与 $y$ 独立
$\text{D.}$ 变量 $x$ 与 $y$ 独立,这个结论犯错误的概率不超过 0.01
某种产品的广告费支出x与销售额y(单位:万元)之间的关系如表:
$y$ 与 $x$ 的线性回归方程为 $\hat{y}=6.5 x+17.5$ ,当广告支出 6 万元时,随机误差的残差为()
$\text{A.}$ -5
$\text{B.}$ -5.5
$\text{C.}$ -6
$\text{D.}$ -6.5
两个变量的相关关系有(1)正相关;(2)负相关;(3)不相关,则下列散点图从左到右分别反映的变量间的相关关系是( )
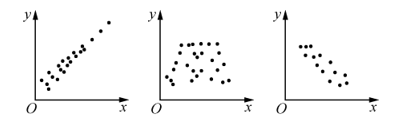
$\text{A.}$ (1)(2)(3)
$\text{B.}$ (2)(3)(1)
$\text{C.}$ (2)(1)(3)
$\text{D.}$ (1)(3)(2)
已知变量 $x$ 和 $y$ 满足关系 $y=-0.1 x+1$ ,变量 $y$ 与 $z$ 正相关,则下列结论中正确的是()
$\text{A.}$ $x$ 与 $y$ 正相关,$x$ 与 $z$ 负相关
$\text{B.}$ $x$ 与 $y$ 正相关,$x$ 与 $z$ 正相关
$\text{C.}$ $x$ 与 $y$ 负相关,$x$ 与 $z$ 负相关
$\text{D.}$ $x$ 与 $y$ 负相关,$x$ 与 $z$ 正相关
蟋蟀鸣叫可以说是大自然优美、和谐的音乐,殊不知蟋蟀鸣叫的频率 $x$(每分钟鸣叫的次数)与气温 $y$(单位:$\left.{ }^{\circ} C \right)$ 存在着较强的线性相关关系.某地观测人员根据如表的观测数据,建立了 $y$ 关于 $x$ 的线性回归方程 $\hat{y}=0.25 x+k$ ,则下列说法不正确的是

$\text{A.}$ $k$ 的值是 20
$\text{B.}$ 变量 $x, y$ 呈正相关关系
$\text{C.}$ 若 $x$ 的值增加 1 ,则 $y$ 的值约增加 0.25
$\text{D.}$ 当蟋蟀 52 次/分鸣叫时,该地当时的气温预报值为 $33.5^{\circ} C$
在对人们休闲方式的一次调查中,根据数据建立如下的 列联表:
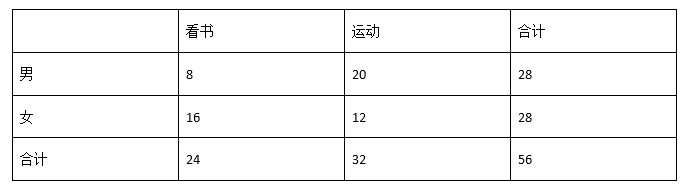
根据表中数据,得到 $K^2=\frac{56 \times(8 \times 12-16 \times 20)^2}{28 \times 28 \times 24 \times 32} \approx 4.667$ ,所以我们至少有 的把握判定休闲方式
与性别有关系.(参考数据:$\left.P\left(K^2 \geq 3.841\right) \approx 0.05, P\left(K^2 \geq 6.635\right) \approx 0.01\right)$
$\text{A.}$ $99 \%$
$\text{B.}$ $95 \%$
$\text{C.}$ $1 \%$
$\text{D.}$ $5 \%$
多选题 (共 1 题 ),每题有多个选项正确
研究变量 $x, y$ 得到一组样本数据,进行回归分析,以下说法正确的是
$\text{A.}$ 残差平方和越大的模型,拟合的效果越好
$\text{B.}$ 用决定系数 $R^2$ 来刻画回归效果,$R^2$ 越大说明拟合效果越好
$\text{C.}$ 在经验回归方程 $\hat{y}=0.2 x+0.5$ 中,当解释变量 $x$ 每增加 1 个单位时,相应观测值 $y$ 增加 0.2 个单位
$\text{D.}$ 经验回归直线一定经过样本中心点 $(\bar{x}, \bar{y})$
填空题 (共 1 题 ),请把答案直接填写在答题纸上
为了判断高中三年级学生是否选修文科与性别的关系,现随机抽取 50 名学生,得到如下 $2 \times 2$ 列联表:
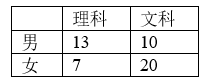
已知 $P\left(K^2 \geqslant 3.841\right) \approx 0.05, P\left(K^2 \geqslant 5.024\right) \approx 0.025$ .根据表中数据,得到 $K^2$ 的观测值 $k= \frac{50 \times(13 \times 20-10 \times 7)^2}{23 \times 27 \times 20 \times 30} \approx 4.844$ ,则认为选修文科与性别有关系出错的可能性为 $\qquad$
解答题 (共 8 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行调研,随机抽查了 100 天空气中的PM2.5和 $SO _2$浓度(单位:$\mu g / m ^3$ ),得下表:
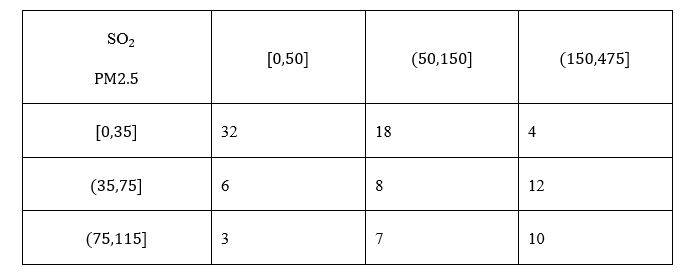
(1)估计事件“该市一天空气中PM2.5浓度不超过75,且$SO_2$浓度不超过150”的概率;
(2)根据所给数据,完成下面的2×2列联表:
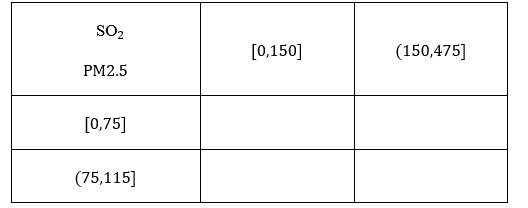
(3)根据(2)中的列联表,判断是否有99%的把握认为该市一天空气中PM2.5浓度与$SO_2$浓度有关?
附
某网络电视剧已开播一段时间,其每日播放量有如下统计表:
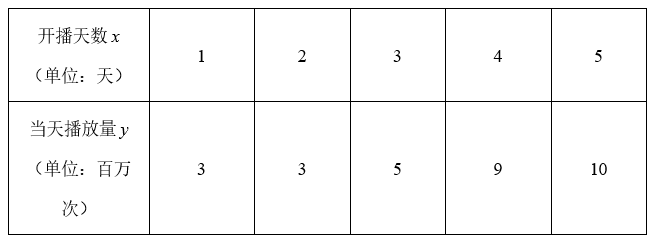
(1)请用线性回归模型拟合 $y$ 与 $x$ 的关系,并用相关系数加以说明;
(2)假设开播后的两周内(除前 5 天),当天播放量 $y$ 与开播天数 $x$ 服从(1)中的线性关系.若每百万播放量可为制作方带来 0.7 万元的收益,且每开播一天需支出 1 万元的广告费,估计制作方在该剧开播两周内获得的利润.
参考公式:$r=\frac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sqrt{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2} \sqrt{\sum_{i=1}^n\left(y_i-\bar{y}\right)^2}}, \hat{b}=\frac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2}, \hat{a}=\bar{y}-\hat{b} \bar{x}$ .参考数据:$\sum_{i=1}^5 x_i y_i=110, \sum_{i=1}^5 x_i^2=55, \sum_{i=1}^5 y_i^2=224, \sqrt{110} \approx 10.5$ .
注:①一般地,相关系数r的绝对值在0.95以上(含0.95)认为线性相关性较强;否则,线性相关性较弱.②利润=收益-广告费.
现在养宠物已经成为一件再正常不过的事情了,尤其是对某些人来说,养宠物是他们生活中非常重要的一件事情,他们还将自己的宠物当成是家人.某机构随机抽取了100名养宠物的人,对他们养宠物的原因进行了调查,根据调查结果,得到如下表数据:
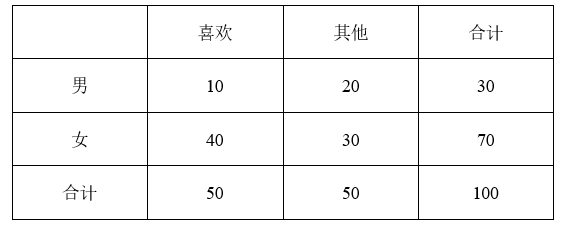
(1)根据表中调查数据,并依据 $\alpha=0.05$ 的独立性检验,能否认为是否是因为喜欢宠物而养宠物与性别有关?
(2)若从这 100 人中,按性别采用分层抽样的方法抽取 10 人,再从这 10 人中随机抽取 4 人,记抽到的男性人数为 $X$ ,求 $X$ 的分布列与期望.
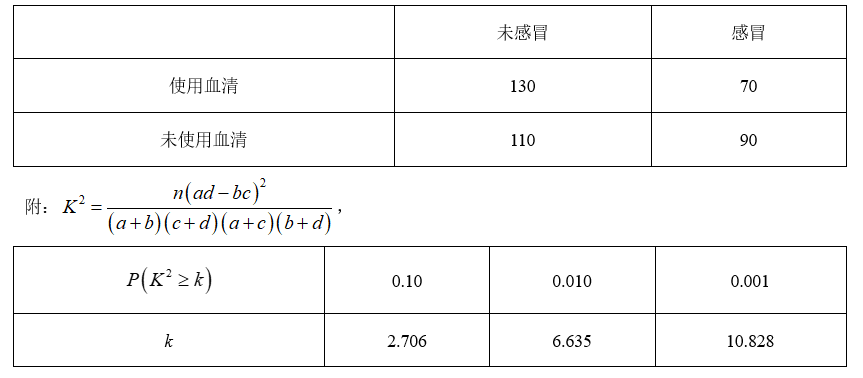
参考公式:$\chi^2=\frac{n(a d-b c)^2}{(a+b)(c+d)(a+c)(b+d)}$ ,其中 $n=a+b+c+d$ .
参考数据:
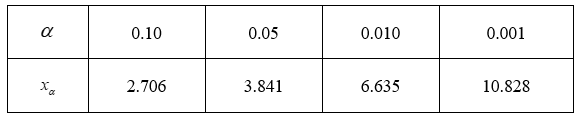
在200人身上试验某种血清预防感冒的作用,把他们1年中的感冒记录与另外200名未用血清的人的感冒记录进行比较,结果如下表所示.问:是否有90%的把握认为该种血清对预防感冒有作用?
强基计划主要选拔培养有志于服务国家重大战略需求且综合素质或基础学科拔尖的学生,聚焦高端芯片与软件、智能科技、新材料、先进制造和国家安全等关键领域,由有关高校结合自身办学特色,合理安排招生.强基计划的校考由试点高校自主命题,校考过程中通过笔试才能进入面试环节.
(1)某研究机构为了更好地服务于高三学生,随机抽取了某校5名高三学生,对其记忆力测试指标 和分析判断力测试指标 进行统计分析,得到下表数据:
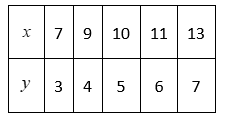
请用线性相关系数判断该组数据中 $y$ 与 $x$ 之间的关系是否可用线性回归模型进行拟合;(精确到 0.01 )
(2)现有甲、乙两所高校的笔试环节都设有三门考试科目,某考生参加每门科目考试是否通过相互独立.若该考生报考甲高校,每门笔试科目通过的概率均为 $\frac{3}{5}$ ;该考生报考乙高校,每门笔试科目通过的概率依次为 $m, \frac{1}{3}, \frac{4}{5}$ ,其中 $0 < m < 1$ .若该考生只能报考甲、乙两所高校中的一所,以笔试中通过的科目数的数学期望为依据作出决策,得知该考生更有希望通过乙大学的笔试,求 $m$ 的取值范围.
参考数据:$\sum_{i=1}^5 x_i^2=520, \sum_{i=1}^5 y_i^2=135, \sqrt{2} \approx 1.414$ ;
参考公式:线性相关系数:$r=\frac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sqrt{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2 \sum_{i=1}^n\left(y_i-\bar{y}\right)^2}}$ .一般地,$|r|>0.75$ 时,认为两个变量之间存在较强的线性相关关系。
大学生赵敏利用寒假参加社会实践,对机械销售公司7月份至12月份销售某种机械配件的销售量及销售单价进行了调查,销售单价x和销售量y之间的一组数据如表所示:
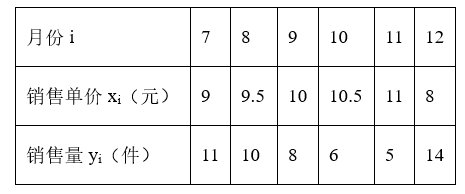
(1)根据 7 至 11 月份的数据,求出 y 关于 x 的回归直线方程;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过 0.5 元,则认为所得到的回归直线方程是理想的,试问(1)中所得到的回归直线方程是否理想?
(3)预计在今后的销售中,销售量与销售单价仍然服从(1)中的关系,若该种机器配件的成本是 2.5 元/件,那么该配件的销售单价应定为多少元才能获得最大利润?(注:利润=销售收入-成本).
参考公式:回归直线方程 $\$=\$ x+\$$ ,其中 $b =\frac{\sum_{ i =1}^{ n } x _{ i } y _{ i }- n \cdot \overline{ x } \cdot \overline{ y }}{\sum_{ i =1}^{ n } x _{ i }^2- n \overline{ x }^2}$ ,参考数据:$\sum_{ i =1}^5 x _{ i } y _{ i }=392, \sum_{ i =1}^{ n } x _{ i }^2=502.5$ .
为了了解一个智力游戏是否与性别有关,从某地区抽取男女游戏玩家各 名,其中游戏水平分为高级和非高级两种.
(1)根据题意完善下列 列联表,依据小概率值α=0.01的独立性检验,能否认为智力游戏水平高低与性别有关联
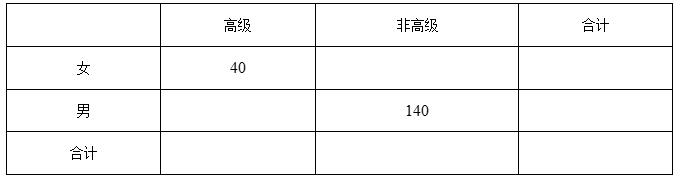
(2)按照性别用分层抽样的方法从这些人中抽取10 人,从这 10人中抽取 3人作为游戏参赛选手;
(ⅰ)若甲入选了10 人名单,求甲成为参赛选手的概率;
(ⅱ)设抽取的 名选手中女生的人数为 X,求X 的分布列和期望.
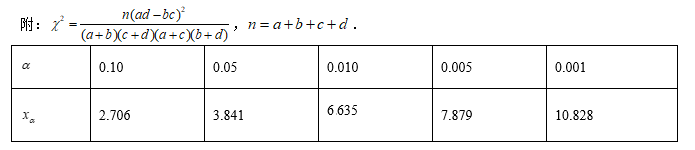
某校组建了足球社团.为了解学生喜欢足球是否与性别有关,随机抽取了男、女同学各100名进行调查,统计得出的数据如下表:
(1)根据所给数据完成上表,试根据小概率值 $\alpha=0.001$ 的独立性检验,分析该校学生喜欢足球与性别是否有关。
(2)社团指导老师从喜欢足球的学生中抽取了 2 名男生和 1 名女生示范点球,已知男生进球的概率为 $\frac{3}{4}$ ,女生进球的概率为 $\frac{1}{3}$ ,每人踢球一次,假设各人踢球相互独立,求 3 人进球总次数的分布列和数学期望.