大学生赵敏利用寒假参加社会实践，对机械销售公司7月份至12月份销售某种机械配件的销售量及销售单价进行了调查，销售单价x和销售量y之间的一组数据如表所示：

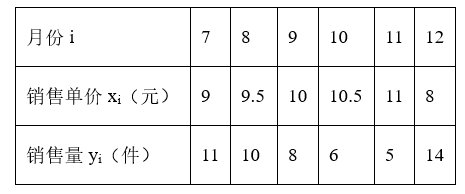
（1）根据 7 至 11 月份的数据，求出 y 关于 x 的回归直线方程；
（2）若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过 0.5 元，则认为所得到的回归直线方程是理想的，试问（1）中所得到的回归直线方程是否理想？
（3）预计在今后的销售中，销售量与销售单价仍然服从（1）中的关系，若该种机器配件的成本是 2.5 元／件，那么该配件的销售单价应定为多少元才能获得最大利润？（注：利润＝销售收入－成本）．

参考公式：回归直线方程 $\$=\$ x+\$$ ，其中 $b =\frac{\sum_{ i =1}^{ n } x _{ i } y _{ i }- n \cdot \overline{ x } \cdot \overline{ y }}{\sum_{ i =1}^{ n } x _{ i }^2- n \overline{ x }^2}$ ，参考数据：$\sum_{ i =1}^5 x _{ i } y _{ i }=392, \sum_{ i =1}^{ n } x _{ i }^2=502.5$ ．