某网络电视剧已开播一段时间，其每日播放量有如下统计表：

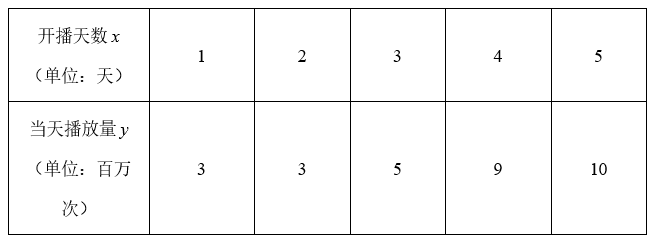
（1）请用线性回归模型拟合 $y$ 与 $x$ 的关系，并用相关系数加以说明；
（2）假设开播后的两周内（除前 5 天），当天播放量 $y$ 与开播天数 $x$ 服从（1）中的线性关系．若每百万播放量可为制作方带来 0.7 万元的收益，且每开播一天需支出 1 万元的广告费，估计制作方在该剧开播两周内获得的利润．

参考公式：$r=\frac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sqrt{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2} \sqrt{\sum_{i=1}^n\left(y_i-\bar{y}\right)^2}}, \hat{b}=\frac{\sum_{i=1}^n\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}{\sum_{i=1}^n\left(x_i-\bar{x}\right)^2}, \hat{a}=\bar{y}-\hat{b} \bar{x}$ ．参考数据：$\sum_{i=1}^5 x_i y_i=110, \sum_{i=1}^5 x_i^2=55, \sum_{i=1}^5 y_i^2=224, \sqrt{110} \approx 10.5$ ．
注：①一般地，相关系数r的绝对值在0.95以上（含0.95）认为线性相关性较强；否则，线性相关性较弱.②利润＝收益－广告费.