单选题 (共 4 题 ),每题只有一个选项正确
长方体 $A B C D-A_1 B_1 C_1 D_1$ 中,$A B=1, A D=A A_1=2, E$ 为棱 $A A_1$ 上的动点,平面 $B E D_1$ 交棱 $C C_1$ 于 $F$ ,则四边形 $B E D_1 F$ 的周长的最小值为( )
$\text{A.}$ $4 \sqrt{3}$
$\text{B.}$ $2 \sqrt{13}$
$\text{C.}$ $2(\sqrt{2}+\sqrt{5})$
$\text{D.}$ $2+4 \sqrt{2}$
已知四面体 $A B C D$ 的一个平面展开图如图所示,其中四边形 $A E F D$ 是边长为 $2 \sqrt{2}$ 的菱形,$B, C$ 分别为 $A E$ , $F D$ 的中点,$B D=2 \sqrt{2}$ ,则在该四面体中
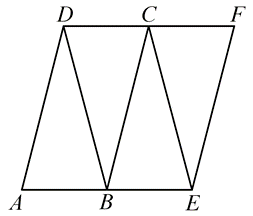
$\text{A.}$ $B E \perp C D$
$\text{B.}$ $B E$ 与平面 $D C E$ 所成角的余弦值为 $\frac{\sqrt{210}}{15}$
$\text{C.}$ 四面体 $A B C D$ 的内切球半径为 $\frac{\sqrt{105}}{30}$
$\text{D.}$ 四面体 $A B C D$ 的外接球表面积为 $9 \pi$
如图,四边形 $A B C D$ 是边长为 2 的正方形,$E$ 为 $A B$ 的中点,将 $\square A E D$ 沿 $D E$ 所在的直线翻折,使 $A$ 与 $A^{\prime}$ 重合,得到四棱锥 $A^{\prime}-B C D E$ ,则在翻折的过程中
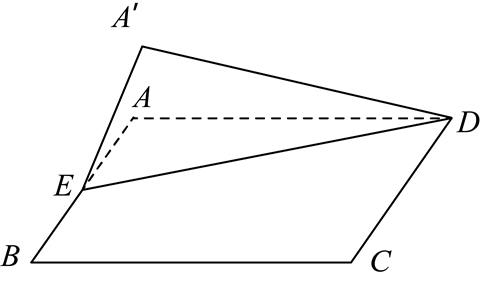
$\text{A.}$ $D E \perp A A^{\prime}$
$\text{B.}$ 存在某个位置,使得 $A^{\prime} E \perp C D$
$\text{C.}$ 存在某个位置,使得 $A^{\prime} B / / D E$
$\text{D.}$ 存在某个位置,使四棱锥 $A^{\prime}-B C D E$ 的体积为 1
在边长为 6 的正三角形 $A B C$ 中 $M, N$ 分别为边 $A B, A C$ 上的点,且满足 $\frac{A M}{A B}=\frac{A N}{A C}=\lambda$ ,把 $\triangle A M N$ 沿着 $M N$翻折至 $A^{\prime} M N$ 位置,则下列说法中正确的有
$\text{A.}$ 在翻折过程中,在边 $A^{\prime} N$ 上存在点 $P$ ,满足 $C P / /$ 平面 $A^{\prime} B M$
$\text{B.}$ 若 $\frac{1}{2} < \lambda < 1$ ,则在翻折过程中的某个位置,满足平面 $A^{\prime} B C \perp$ 平面 $B C N M$
$\text{C.}$ 若 $\lambda=\frac{1}{2}$ 且二面角 $A^{\prime}-M N-B$ 的大小为 $120^{\circ}$ ,则四棱锥 $A^{\prime}-B C N M$ 的外接球的表面积为 $61 \pi$
$\text{D.}$ 在翻折过程中,四棱锥 $A^{\prime}-B C N M$ 体积的最大值为 $6 \sqrt{3}$
多选题 (共 1 题 ),每题有多个选项正确
如图,一张长、宽分别为 $\sqrt{2}, 1$ 的矩形纸,$A, B, C, D$ 分别是其四条边的中点.现将其沿图中虚线折起,使得 $P_1, P_2, P_3, P_4$ 四点重合为一点 $P$ ,从而得到一个多面体,则
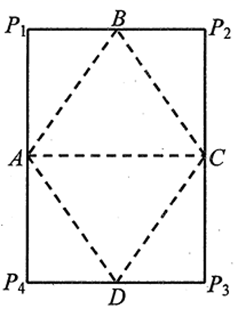
$\text{A.}$ 在该多面体中,$B D=\sqrt{2}$
$\text{B.}$ 该多面体是三棱锥
$\text{C.}$ 在该多面体中,平面 $B A D \perp$ 平面 $B C D$
$\text{D.}$ 该多面体的体积为 $\frac{1}{12}$
填空题 (共 3 题 ),请把答案直接填写在答题纸上
如图,在三棱锥 $P-A B C$ 的平面展开图中,$A C=1, A B=A D=\sqrt{3}, A B \perp A C, A B \perp A D, \angle C A E=30^{\circ}$ ,则 $\cos$ $\angle F C B=$
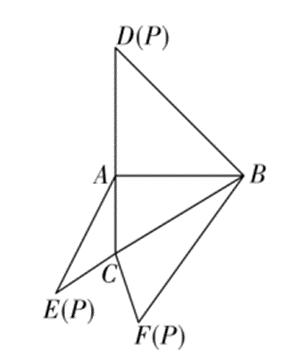
如图,$A B C D$ 是一块直角梯形加热片,$A B / / C D, \angle D A B=60^{\circ}, A B=A D=4 dm$ .现将 $\triangle B C D$ 沿 $B D$ 折起,成为二面角 $A-B D-C$ 是 $90^{\circ}$ 的加热零件,则 $A C$ 间的距离是 $\qquad$ dm ;为了安全,把该零件放进一个球形防护罩,则球形防护罩的表面积的最小值是 $\qquad$ $dm ^2$ .(所有器件厚度忽略不计)
如图,$D E$ 是边长为 4 的等边三角形 $A B C$ 的中位线,将 $\square A D E$ 沿 $D E$ 折起,使得点 A 与 $P$ 重合,平面 $P D E \perp$平面 $B C D E$ ,则四棱锥 $P-B C D E$ 外接球的表面积是
