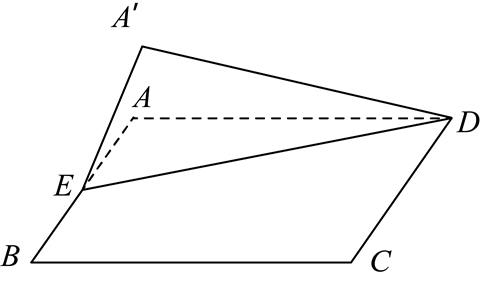
如图,四边形 $A B C D$ 是边长为 2 的正方形,$E$ 为 $A B$ 的中点,将 $\square A E D$ 沿 $D E$ 所在的直线翻折,使 $A$ 与 $A^{\prime}$ 重合,得到四棱锥 $A^{\prime}-B C D E$ ,则在翻折的过程中
A
$D E \perp A A^{\prime}$
B
存在某个位置,使得 $A^{\prime} E \perp C D$
C
存在某个位置,使得 $A^{\prime} B / / D E$
D
存在某个位置,使四棱锥 $A^{\prime}-B C D E$ 的体积为 1
E
F