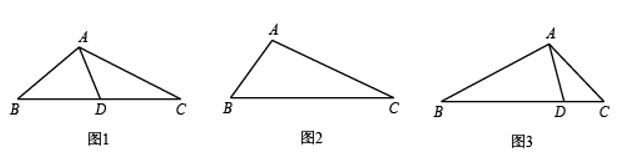
定义：从三角形（不是等腰三角形）的一个顶点引出一条射线与对边相交，顶点与交点所连线段把这个三角形分割成两个小三角形，如果其中一个为等腰三角形，另一个与原三角形相似，我么就把这条线段叫做这个三角形的＂华丽分割线＂．

例如：如图 1，$A D$ 把 $\triangle A B C$ 分成 $\triangle A B D$ 和 $\triangle A D C$ ，若 $\triangle A B D$ 是等腰三角形，且 $\triangle A D C \sim \triangle B A C$ ，那么 $A D$就是 $\triangle A B C$ 的＂华丽分割线＂．
【定义感知】
（1）如图 1，在 $\triangle A B C$ 中，$\angle B=40^{\circ}, \angle B A C=110^{\circ}, A B=B D$ ．求证：$A D$ 是 $\triangle A B C$ 的＂华丽分割线＂．
【问题解决】
（2） ① 如图 2，在 $\triangle A B C$ 中，$\angle B=46^{\circ}, A D$ 是 $\triangle A B C$ 的＂华丽分割线＂，且 $\triangle A B D$ 是等腰三角形，则 $\angle C$ 的度数是 $\qquad$ ；
② 如图 3，在 $\triangle A B C$ 中，$A B=2, A C=\sqrt{3}, A D$ 是 $\triangle A B C$ 的＂华丽分割线＂，且 $\triangle A B D$ 是以 $A D$ 为底边的等腰三角形，求华丽分割线 $A D$ 的长．

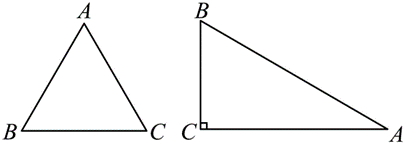
我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）．如图回，在 $\triangle A B C$ 中，$A B=A C$ ，顶角 $A$ 的正对记作 $sad ^A$ ，这时 $sad ^A=\frac{\text { 底边 }}{\text { 腰 }}=\frac{B C}{A B}$ ，容易知道一个角的大小与这个角的正对值也是相互唯一确定的。根据上述角的正对定义，解答下列问题：
${ }^{(1)}{ }_{\text {sad }} 60^{\circ}=$ $\qquad$ ，${ }_{s a d} 90^{\circ}=$ $\qquad$ ；
（2）如图，已知 ${ }_{\sin } A=\frac{3}{5}$ ，其中 $\angle A$ 为锐角，试求 ${ }_{ sad } A$ 的值．

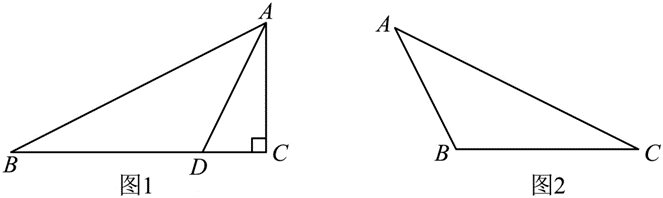
在一个三角形中，如果有两个内角 $\alpha$ 与 $\beta$ 满足 $2 \alpha+\beta=90^{\circ}$ ，那么我们称这样的三角形为＂亚直角三角形＂．根据这个定义，显然 $\alpha+\beta < 90^{\circ}$ ，则这个三角形的第三个角为 $180^{\circ}-(\alpha+\beta)>90^{\circ}$ ，这就是说＂亚直角三角形＂是特殊的钝角三角形．
（1）【尝试运用】：若某三角形是＂亚直角三角形＂，且一个内角为 $100^{\circ}$ ，请求出它的两个锐角的度数；
（2）【尝试运用】：如图 1，在 $Rt \triangle A B C$ 中，$\angle A C B=90^{\circ}, A C=4, B C=8$ ，点 $D$ 在边 $B C$ 上，连接 $A D$ ，且 $A D$ 不平分 $\angle B A C$ ．若 $\triangle A B D$ 是＂亚直角三角形＂，求线段 $A D$ 的长；
（3）【素养提升】：如图 2，在钝角 $\triangle A B C$ 中，$\angle A B C>90^{\circ}, A B=5, B C=3 \sqrt{5}, \triangle A B C$ 的面积为 15 ，求证：$\triangle A B C$ 是＂亚直角三角形＂．

定义：两组邻边分别相等的四边形叫做筝形．

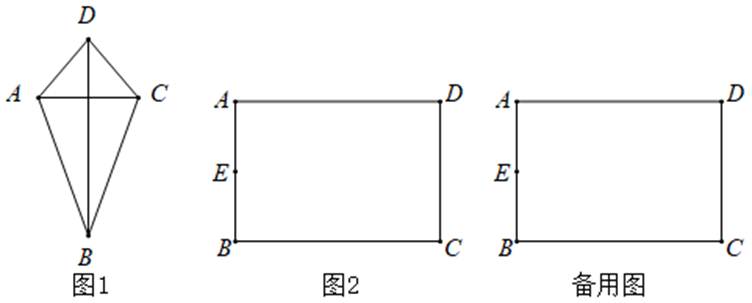
（1）问题发现：如图 1，箏形 $A B C D$ 中，$A D=C D, A B=C B$ ，若 $A C+B D=12$ ，求筝形 $A B C D$ 的面积的最大值；
（2）问题解决：如图 2 是一块矩形铁片 $A B C D$ ，其中 $A B=60$ 厘米，$B C=90$ 厘米，李优想从这块铁片中裁出一个筝形 $E F G H$ ，要求点 $E$ 是 $A B$ 边的中点，点 $F 、 G 、 H$ 分别在 $B C 、 C D 、 A D$ 上（含端点），是否存在一种裁剪方案，使得筝形 $E F G H$ 的面积最大？若存在，求出筝形 $E F G H$ 的面积最大值，若不存在，请说明理由．

我们定义：有一组邻角相等的凸四边形叫做＂等邻角四边形＂．例如：如图（1），$\angle B=\angle C$ ，则四边形 $A B C D$为＂等邻角四边形＂。

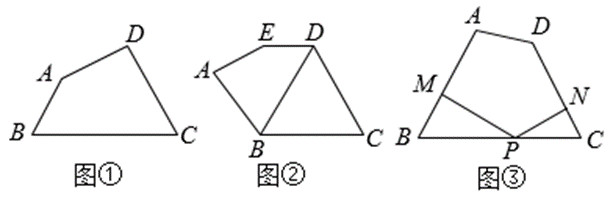
（1）定义理解：以下平面图形中，是等邻角四边形的是 $\qquad$ ．
① 平行四边形；
② 矩形；
③ 菱形；
④等腰梯形．
（2）深入探究：
① 已知四边形 $A B C D$ 为＂等邻角四边形＂，且 $\angle A=120^{\circ}, \angle B=100^{\circ}$ ，则 $\angle D=$ $\qquad$ ．
② 如图 ② ，在五边形 $A B C D E$ 中，$D E \| B C$ ，对角线 $B D$ 平分 $\angle A B C$ ，求证：四边形 $A B D E$ 为等邻角四边形．
（3）拓展应用：如图 ③ ，在等邻角四边形 $A B C D$ 中，$\angle B=\angle C$ ，点 $P$ 为边 $B C$ 上的一动点，过点 $P$ 作 $P M \perp$ $A B, P N \perp C D$ ，垂足分别为 $M, N$ ．在点 $P$ 的运动过程中，$P M+P N$ 的值是否会发生变化？请说明理由．

定义：如果一个三角形有一个内角的平分线与这个角的对边的夹角是60°，那么称该三角形为“特异角平分三角形”，这条角平分线称为“特异角平分线”．

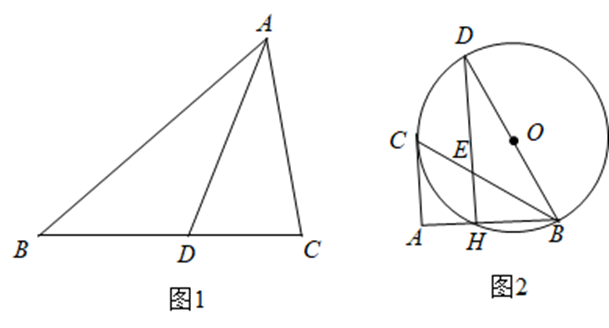
（1）如图 1，$\triangle A B C$ 是一个＂特异角平分三角形＂，$A D$ 是一条＂特异角平分线＂
① 当 $\angle C=90^{\circ}$ 时，试求 $A D: B D$ 的值．
② 在 $\triangle A B C$ 中，过点 $D$ 作 $D E \perp A B$ 于点 $E$ ，延长至点 $H, H E=D E$ ，若 $D E: A E=\sqrt{3}: 3$ ，证明：$\triangle A H E \cong$ $\triangle A D C$ ．
（2）如图 2．$B D$ 是 $\odot O$ 的直径，$A C$ 是 $\odot O$ 的切线，点 $C$ 为切点，$A B \perp A C$ 于点 $A$ 且交 $\odot O$ 于点 $H$ ，连接 $D H$交 $B C$ 于点 $E, B D=4, A B=3$ ．试证明 $\triangle D B H$ 是一个＂特异角平分三角形＂．

定义：若一个圆内接四边形的两条对角线互相垂直，则称这个四边形为圆美四边形．


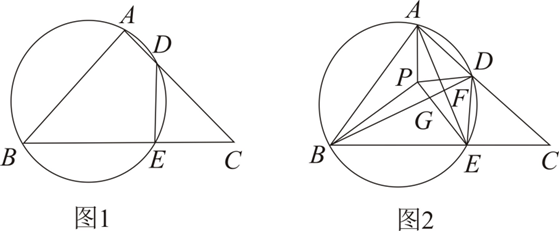
（1）请在特殊四边形中找出一个圆美四边形，该四边形的名称是 $\qquad$ ；
（2）如图 1，在等腰 Rt $\triangle A B C$ 中，$\angle B A C=90^{\circ}$ ，经过点 $A 、 B$ 的 $\odot O$ 交 $A C$ 边于点 $D$ ，交 $B C$ 于点 $E$ ，连接 $D E$ ，若四边形 $A B E D$ 为圆美四边形，则 $\frac{A B}{D E}$ 的值是 $\qquad$
（3）如图 2，在 $\triangle A B C$ 中，经过点 $A 、 B$ 的 $\odot O$ 交 $A C$ 边于点 $D$ ，交 $B C$ 于点 $E$ ，连接 $A E 、 B D$ 交于点 $F$ ，若在四边形 $A B E D$ 的内部存在一点 $P$ ，使得 $\angle P B C=\angle A D P=\alpha$ ，连接 $P E$ 交 $B D$ 于点 $G$ ，连接 $P A$ ，若 $P A \perp P D, P B \perp P E$ ．
① 试说明：四边形 $A B E D$ 为圆美四边形；
② 若 $\tan \alpha=\frac{2}{3}, P A+P E=8, \frac{C D}{B C}=\frac{\sqrt{3}}{3}$ ，求 $D E$ 的最小值．