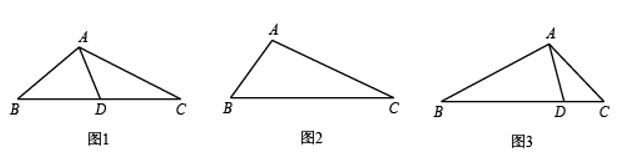
定义：从三角形（不是等腰三角形）的一个顶点引出一条射线与对边相交，顶点与交点所连线段把这个三角形分割成两个小三角形，如果其中一个为等腰三角形，另一个与原三角形相似，我么就把这条线段叫做这个三角形的＂华丽分割线＂．

例如：如图 1，$A D$ 把 $\triangle A B C$ 分成 $\triangle A B D$ 和 $\triangle A D C$ ，若 $\triangle A B D$ 是等腰三角形，且 $\triangle A D C \sim \triangle B A C$ ，那么 $A D$就是 $\triangle A B C$ 的＂华丽分割线＂．
【定义感知】
（1）如图 1，在 $\triangle A B C$ 中，$\angle B=40^{\circ}, \angle B A C=110^{\circ}, A B=B D$ ．求证：$A D$ 是 $\triangle A B C$ 的＂华丽分割线＂．
【问题解决】
（2） ① 如图 2，在 $\triangle A B C$ 中，$\angle B=46^{\circ}, A D$ 是 $\triangle A B C$ 的＂华丽分割线＂，且 $\triangle A B D$ 是等腰三角形，则 $\angle C$ 的度数是 $\qquad$ ；
② 如图 3，在 $\triangle A B C$ 中，$A B=2, A C=\sqrt{3}, A D$ 是 $\triangle A B C$ 的＂华丽分割线＂，且 $\triangle A B D$ 是以 $A D$ 为底边的等腰三角形，求华丽分割线 $A D$ 的长．