定义：若一个圆内接四边形的两条对角线互相垂直，则称这个四边形为圆美四边形．


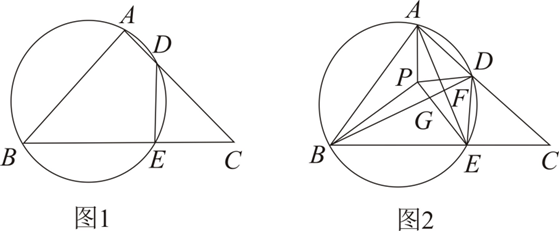
（1）请在特殊四边形中找出一个圆美四边形，该四边形的名称是 $\qquad$ ；
（2）如图 1，在等腰 Rt $\triangle A B C$ 中，$\angle B A C=90^{\circ}$ ，经过点 $A 、 B$ 的 $\odot O$ 交 $A C$ 边于点 $D$ ，交 $B C$ 于点 $E$ ，连接 $D E$ ，若四边形 $A B E D$ 为圆美四边形，则 $\frac{A B}{D E}$ 的值是 $\qquad$
（3）如图 2，在 $\triangle A B C$ 中，经过点 $A 、 B$ 的 $\odot O$ 交 $A C$ 边于点 $D$ ，交 $B C$ 于点 $E$ ，连接 $A E 、 B D$ 交于点 $F$ ，若在四边形 $A B E D$ 的内部存在一点 $P$ ，使得 $\angle P B C=\angle A D P=\alpha$ ，连接 $P E$ 交 $B D$ 于点 $G$ ，连接 $P A$ ，若 $P A \perp P D, P B \perp P E$ ．
① 试说明：四边形 $A B E D$ 为圆美四边形；
② 若 $\tan \alpha=\frac{2}{3}, P A+P E=8, \frac{C D}{B C}=\frac{\sqrt{3}}{3}$ ，求 $D E$ 的最小值．