定义：两组邻边分别相等的四边形叫做筝形．

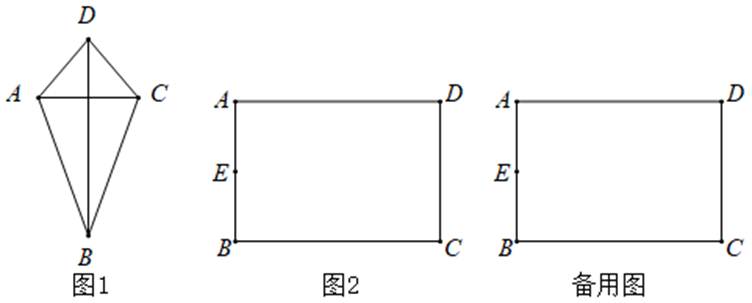
（1）问题发现：如图 1，箏形 $A B C D$ 中，$A D=C D, A B=C B$ ，若 $A C+B D=12$ ，求筝形 $A B C D$ 的面积的最大值；
（2）问题解决：如图 2 是一块矩形铁片 $A B C D$ ，其中 $A B=60$ 厘米，$B C=90$ 厘米，李优想从这块铁片中裁出一个筝形 $E F G H$ ，要求点 $E$ 是 $A B$ 边的中点，点 $F 、 G 、 H$ 分别在 $B C 、 C D 、 A D$ 上（含端点），是否存在一种裁剪方案，使得筝形 $E F G H$ 的面积最大？若存在，求出筝形 $E F G H$ 的面积最大值，若不存在，请说明理由．