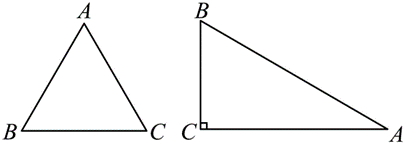
我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）．如图回，在 $\triangle A B C$ 中，$A B=A C$ ，顶角 $A$ 的正对记作 $sad ^A$ ，这时 $sad ^A=\frac{\text { 底边 }}{\text { 腰 }}=\frac{B C}{A B}$ ，容易知道一个角的大小与这个角的正对值也是相互唯一确定的。根据上述角的正对定义，解答下列问题：
${ }^{(1)}{ }_{\text {sad }} 60^{\circ}=$ $\qquad$ ，${ }_{s a d} 90^{\circ}=$ $\qquad$ ；
（2）如图，已知 ${ }_{\sin } A=\frac{3}{5}$ ，其中 $\angle A$ 为锐角，试求 ${ }_{ sad } A$ 的值．