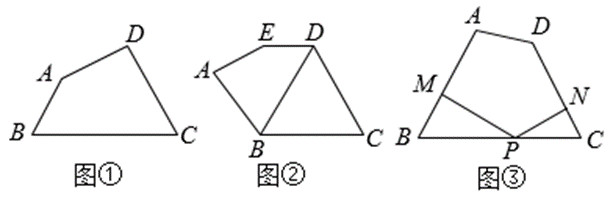
我们定义：有一组邻角相等的凸四边形叫做＂等邻角四边形＂．例如：如图（1），$\angle B=\angle C$ ，则四边形 $A B C D$为＂等邻角四边形＂。

（1）定义理解：以下平面图形中，是等邻角四边形的是 $\qquad$ ．
① 平行四边形；
② 矩形；
③ 菱形；
④等腰梯形．
（2）深入探究：
① 已知四边形 $A B C D$ 为＂等邻角四边形＂，且 $\angle A=120^{\circ}, \angle B=100^{\circ}$ ，则 $\angle D=$ $\qquad$ ．
② 如图 ② ，在五边形 $A B C D E$ 中，$D E \| B C$ ，对角线 $B D$ 平分 $\angle A B C$ ，求证：四边形 $A B D E$ 为等邻角四边形．
（3）拓展应用：如图 ③ ，在等邻角四边形 $A B C D$ 中，$\angle B=\angle C$ ，点 $P$ 为边 $B C$ 上的一动点，过点 $P$ 作 $P M \perp$ $A B, P N \perp C D$ ，垂足分别为 $M, N$ ．在点 $P$ 的运动过程中，$P M+P N$ 的值是否会发生变化？请说明理由．