定义：如果一个三角形有一个内角的平分线与这个角的对边的夹角是60°，那么称该三角形为“特异角平分三角形”，这条角平分线称为“特异角平分线”．

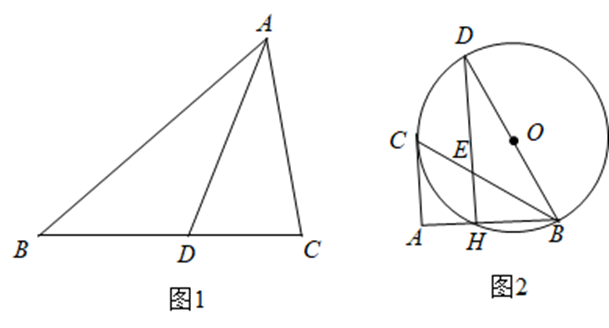
（1）如图 1，$\triangle A B C$ 是一个＂特异角平分三角形＂，$A D$ 是一条＂特异角平分线＂
① 当 $\angle C=90^{\circ}$ 时，试求 $A D: B D$ 的值．
② 在 $\triangle A B C$ 中，过点 $D$ 作 $D E \perp A B$ 于点 $E$ ，延长至点 $H, H E=D E$ ，若 $D E: A E=\sqrt{3}: 3$ ，证明：$\triangle A H E \cong$ $\triangle A D C$ ．
（2）如图 2．$B D$ 是 $\odot O$ 的直径，$A C$ 是 $\odot O$ 的切线，点 $C$ 为切点，$A B \perp A C$ 于点 $A$ 且交 $\odot O$ 于点 $H$ ，连接 $D H$交 $B C$ 于点 $E, B D=4, A B=3$ ．试证明 $\triangle D B H$ 是一个＂特异角平分三角形＂．