单选题 (共 10 题 ),每题只有一个选项正确
$-8$的导数是( )
$\text{A.}$ $-\dfrac{1}{8}$
$\text{B.}$ $-8$
$\text{C.}$ $8$
$\text{D.}$ $\dfrac{1}{8}$
下列运算一定正确的是( )
$\text{A.}$ $a^2+a^2=a^4$
$\text{B.}$ $a^2 • a^4=a^8$
$\text{C.}$ $(a^2)^4=a^8$
$\text{D.}$ $(a+b)^2=a^2+b^2$
下列图形中既是轴对称图形又是中心对称图形的是
$\text{A.}$  扇形
$\text{B.}$
扇形
$\text{B.}$  正方形
$\text{C.}$
正方形
$\text{C.}$  等腰直角三角形
$\text{D.}$
等腰直角三角形
$\text{D.}$  正五边形
正五边形
如图, $A B$ 为 $\odot O$ 的切线, 点 $A$ 为切点, $O B$ 交 $\odot O$ 于点 $C$, 点 $D$ 在 $\odot O$ 上, 连接 $A D 、 C D, O A$, 若 $\angle A D C=35^{\circ}$, 则 $\angle A B O$ 的度数为 ( )
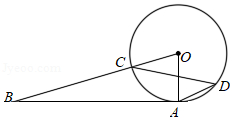
$\text{A.}$ $25^{\circ}$
$\text{B.}$ $20^{\circ}$
$\text{C.}$ $30^{\circ}$
$\text{D.}$ $35^{\circ}$
将抛物线 $y=x^{2}$ 向上平移 3 个单位长度, 再向右平移 5 个单位长度, 所得到的抛物线为 ( )
$\text{A.}$ $y=(x+3)^{2}+5$
$\text{B.}$ $y=(x-3)^{2}+5$
$\text{C.}$ $y=(x+5)^{2}+3$
$\text{D.}$ $y=(x-5)^{2}+3$
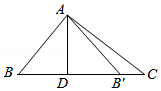
如图, 在 Rt $\triangle A B C$ 中, $\angle B A C=90^{\circ}, \angle B=50^{\circ}, A D \perp B C$, 垂足为 $D, \triangle A D B$ 与 $\triangle A D B^{\prime}$ 关于直线 $A D$ 对称, 点 $B$ 的对称点是点 $B^{\prime}$, 则 $\angle C A B^{\prime}$ 的度数为 ( )
$\text{A.}$ $10^{\circ}$
$\text{B.}$ $20^{\circ}$
$\text{C.}$ $30^{\circ}$
$\text{D.}$ $40^{\circ}$
方程 $\frac{2}{x+5}=\frac{1}{x-2}$ 的解为 ( )
$\text{A.}$ $x=-1$
$\text{B.}$ $x=5$
$\text{C.}$ $x=7$
$\text{D.}$ $x=9$
一个不透明的袋子中装有 9 个小球, 其中 6 个红球、 3 个绿球, 这些小球除颜色外无其他 差别, 从袋子中随机摸出一个小球. 则摸出的小球是红球的概率是 ( )
$\text{A.}$ $\frac{2}{3}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $\frac{1}{3}$
$\text{D.}$ $\frac{1}{9}$
如图, 在 $\triangle A B C$ 中, 点 $D$ 在 $B C$ 边上, 连接 $A D$, 点 $E$ 在 $A C$ 边上, 过点 $E$ 作 $E F / / B C$, 交 $A D$ 于点 $F$, 过点 $E$ 作 $E G / / A B$, 交 $B C$ 于点 $G$, 则下列式子一定正确的是 ( )

$\text{A.}$ $\frac{A E}{E C}=\frac{E F}{C D}$
$\text{B.}$ $\frac{E F}{C D}=\frac{E G}{A B}$
$\text{C.}$ $\frac{A F}{F D}=\frac{B G}{G C}$
$\text{D.}$ $\frac{C G}{B C}=\frac{A F}{A D}$
填空题 (共 11 题 ),请把答案直接填写在答题纸上
在函数 $y=\frac{x}{x-7}$ 中, 自变量 $x$ 的取值范围是 ( )
已知反比例函数 $y=\frac{k}{x}$ 的图象经过点 $(-3,4)$, 则 $k$ 的值为 ( )
计算 $\sqrt{24}+6 \sqrt{\frac{1}{6}}$ 的结果是 ( )
把多项式 $m^{2} n+6 m n+9 n$ 分解因式的结果是 ( )
抛物线 $y=3(x-1)^{2}+8$ 的顶点坐标为 ( )
不等式组 $\left\{\begin{array}{l}\frac{x}{3} \leq-1, \\ 3 x+5 < 2\end{array}\right.$ 的解集是 ( )
一个扇形的面积是 $13 \pi \mathrm{cm}^{2}$, 半径是 $6 \mathrm{~cm}$, 则此扇形的圆心角是
( ) 度.
在 $\triangle A B C$ 中, $\angle A B C=60^{\circ}, A D$ 为 $B C$ 边上的高, $A D=6 \sqrt{3}, C D=1$, 则 $B C$ 的长为 ( )
如图,在菱形ABCD中,对角线AC、BD相交于点O,点E在线段BO上,连接AE,若CD=2BE,∠DAE=∠DEA,EO=1,则线段AE的长为 ( )

先化简, 再求代数式 $\left(1-\frac{2}{x+1}\right) \div \frac{x^{2}-1}{2 x+2}$ 的值, 其中 $x=4 \cos 30^{\circ}-1$.
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
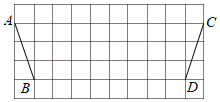
如图, 方格纸中每个小正方形的边长均为 1 , 线段 $A B$ 和线段 $C D$ 的端点均在小 正方形的顶点上.
(1) 在图中画出以 $A B$ 为边的正方形 $A B E F$, 点 $E$ 和点 $F$ 均在小正方形的顶点上;
(2) 在图中画出以 $C D$ 为边的等腰三角形 $C D G$, 点 $G$ 在小正方形的顶点上, 且 $\triangle C D G$ 的周长为 $10+\sqrt{10}$. 连接 $E G$, 请直接写出线段 $E G$ 的长.
为了丰富同学们的课余生活,冬威中学开展以“我最喜欢的课外活动小组”为主题的调查活动,围绕“在绘画、剪纸、舞蹈、书法四类活动小组中,你最喜欢哪一类?(必选且只选一类)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的条形统计图,其中最喜欢绘画小组的学生人数占所调查人数的30%.请你根据图中提供的信息回答下列问题:
(1)在这次调查中,一共抽取了多少名学生?
(2)请通过计算补全条形统计图;
(3)若冬威中学共有800名学生,请你估计该中学最喜欢剪纸小组的学生有多少名.

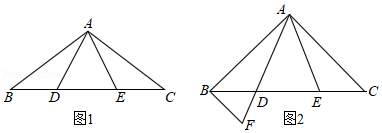
已知: 在 $\triangle A B C$ 中, $A B=A C$, 点 $D 、$ 点 $E$ 在边 $B C$ 上, $B D=C E$, 连接 $A D 、 A E$.
(1) 如图 1, 求证: $A D=A E$;
(2) 如图 2, 当 $\angle D A E=\angle C=45^{\circ}$ 时, 过点 $B$ 作 $B F / / A C$ 交 $A D$ 的延长线于点 $F$, 在不 添加任何辅助线的情况下, 请直接写出图, 2 中的四个等腰三角形, 使写出的每个等腰三 角形的顶角都等于 $45^{\circ}$.
昌云中学计划为地理兴趣小组购买大、小两种地球仪,若购买1个大地球仪和3个小地球仪需用136元;若购买2个大地球仪和1个小地球仪需用132元.
(1)求每个大地球仪和每个小地球仪各多少元;
(2)昌云中学决定购买以上两种地球仪共30个,总费用不超过960元,那么昌云中学最多可以购买多少个大地球仪?
已知: $\odot O$ 是 $\triangle A B C$ 的外接圆, $A D$ 为 $\odot O$ 的直径, $A D \perp B C$, 垂足为 $E$, 连接 $B O$, 延长 $B O$ 交 $A C$ 于点 $F$.
(1) 如图 1, 求证: $\angle B F C=3 \angle C A D$;
(2) 如图 2, 过点 $D$ 作 $D G / / B F$ 交 $\odot O$ 于点 $G$, 点 $H$ 为 $D G$ 的中点, 连接 $O H$, 求证: $B E=O H$;
(3) 如图 3, 在 (2) 的条件下, 连接 $C G$, 若 $D G=D E, \triangle A O F$ 的面积为 $\frac{9 \sqrt{2}}{5}$, 求线段 $C G$ 的长.

已知: 在平面直角坐标系中, 点 $O$ 为坐标原点, 直线 $A B$ 与 $x$ 轴的正半轴交于点 $A$, 与 $y$ 轴 的负半轴交于点 $B, O A=O B$, 过点 $A$ 作 $x$ 轴的垂线与过点 $O$ 的直线相交于点 $C$, 直线 $O C$ 的解析式为 $y=\frac{3}{4} x$, 过点 $C$ 作 $C M \perp y$ 轴, 垂足为 $M, O M=9$.
(1) 如图 1, 求直线 $A B$ 的解析式;
(2) 如图 2, 点 $N$ 在线段 $M C$ 上, 连接 $O N$, 点 $P$ 在线段 $O N$ 上, 过点 $P$ 作 $P D \perp x$ 轴, 垂足为 $D$, 交 $O C$ 于点 $E$, 若 $N C=O M$, 求 $\frac{P E}{O D}$ 的值;
(3) 如图 3, 在 (2) 的条件下, 点 $F$ 为线段 $A B$ 上一点, 连接 $O F$, 过点 $F$ 作 $O F$ 的垂 线交线段 $A C$ 于点 $Q$, 连接 $B Q$, 过点 $F$ 作 $x$ 轴的平行线交 $B Q$ 于点 $G$, 连接 $P F$ 交 $x$ 轴 于点 $H$, 连接 $E H$, 若 $\angle D H E=\angle D P H, G Q-F G=\sqrt{2} A F$, 求点 $P$ 的坐标.
