单选题 (共 3 题 ),每题只有一个选项正确
在空间直角坐标系 $O-x y z$ 中,三张平面
$$
\pi_i: a_i x+b_i y+c_i z=d_i(i=1,2,3)
$$
的位置关系如下图所示.
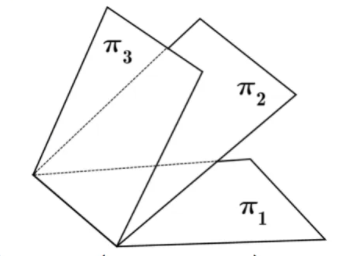
记 $\alpha_i=\left(a_i, b_i, c_i\right), \beta_i=\left(a_i, b_i, c_i, d_i\right)$ ,若 $r\left(\begin{array}{l}\alpha_1 \\ \alpha_2 \\ \alpha_3\end{array}\right)=m, r\left(\begin{array}{l}\beta_1 \\ \beta_2 \\ \beta_3\end{array}\right)=n$ ,则 $(\quad)$
$\text{A.}$ $m=1, n=2$
$\text{B.}$ $m=n=2$
$\text{C.}$ $m=2, n=3$
$\text{D.}$ $m=n=3$
设向量 $\alpha_1=\left(\begin{array}{c}a \\ 1 \\ -1 \\ 1\end{array}\right), \alpha_2=\left(\begin{array}{l}1 \\ 1 \\ b \\ a\end{array}\right), \alpha_3=\left(\begin{array}{c}1 \\ a \\ -1 \\ 1\end{array}\right)$, 若 $\alpha_1, \alpha_2, \alpha_3$ 线性相关,且其中任意两个向量均线性无关,则()
$\text{A.}$ $a=1, b \neq-1$
$\text{B.}$ $a=1, b=-1$
$\text{C.}$ $a \neq-2, b=2$
$\text{D.}$ $a=-2, b=2$
设 $\boldsymbol{A}$ 是秩为 2 的 3 阶矩阵, $\boldsymbol{\alpha}$ 是满足 $\boldsymbol{A} \boldsymbol{\alpha}=0$ 的非零向量,若对满足 $\boldsymbol{\beta}^T \boldsymbol{\alpha}=\mathbf{0}$ 的 3 维向量 $\boldsymbol{\beta}$ ,均有 $\boldsymbol{A} \boldsymbol{\beta}=\boldsymbol{\beta}$ ,则( )
$\text{A.}$ $A^3$ 的迹为 2
$\text{B.}$ $A^3$ 的迹为 5
$\text{C.}$ $A^2$ 的迹为 8
$\text{D.}$ $A^2$ 的迹为 9
填空题 (共 1 题 ),请把答案直接填写在答题纸上
已知 $\boldsymbol{A}=\left(\begin{array}{cc}a+1 & a \\ a & a\end{array}\right)$, 对于任意的实向量 $\alpha=\binom{x_1}{x_2}, \boldsymbol{\beta}=\binom{y_1}{y_2}$ ,都有 $\left(\boldsymbol{\alpha}^T \boldsymbol{A} \boldsymbol{\beta}\right)^2 \leq \boldsymbol{\alpha}^T \boldsymbol{A} \boldsymbol{\alpha} \cdot \boldsymbol{\beta}^T \boldsymbol{A} \boldsymbol{\beta}$ ,则 $\boldsymbol{a}$ 的取值范围是
解答题 (共 1 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知数列 $\left\{x_n\right\},\left\{y_n\right\},\left\{z_n\right\}$ 满足
$$
\begin{aligned}
x_0=-1, y_0 & =0, z_0=2 \text { 且 } \\
& \left\{\begin{array}{l}
x_n=-2 x_{n-1}+2 z_{n-1}, \\
y_n=-2 y_{n-1}-2 z_{n-1} \\
z_n=-6 x_{n-1}-3 y_{n-1}+3 z_{n-1}
\end{array}\right.
\end{aligned}
$$
记 $\alpha_n=\left(\begin{array}{l}x_n \\ y_n \\ z_n\end{array}\right)$ ,写出满足 $\alpha_n=A \alpha_{n-1}$ 的矩阵 $A$ ,并求 $A^n$ 及 $x_n, y_n, z_n(n=1,2, \cdots)$ 的通项表达式.