一、单选题 (共 8 题 ),每题只有一个选项正确
1. 在 这四个数中, 比 -2 小的是
-1
0
-3
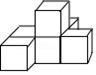
2. 如图是一个由6个相同的正方体组成的立体图形,它的俯视图是
3. 下列运算正确的是
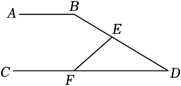
4. 如图,
, 则
的度数为
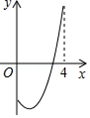
5. 一次函数 与 在同一个平面直角坐标系中, 且 , 则两个图象交点在
第一象限
第二象限
第三象限
第四象限
6. 如图, 在 中, 点 为边 的三等分点, 点 在边 上, 且 , 点 为 与 的交点. 若 , 则 的长为
2
3
7. 如图, 圆
中, 弦
与
交于点
, 点
为
中点,
,则
的度数是

8. 如图是函数
的图象, 直线
轴且过点
, 将该函数在直线
上方的图象沿直线
向下翻折, 在直线
下方的图象保持不变, 得到一个新图象. 若新图象对应的函数的最大值与最小值之差不大于 5 , 则
的取值范围是
或
二、填空题 (共 5 题 ),请把答案直接填写在答题纸上
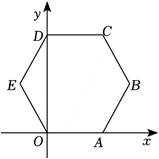
10. 如图, 在正六边形
中, 以点
为原点建立平面直角坐标系, 边
落在
轴上. 若点
的坐标为
, 则点
的坐标为
11. “北斗系统” 是我国自主建设运行的全球卫星导航系统, 国内多个导航地图采用北斗优先定位. 目前, 北斗定位服务日均使用量已超过 24900 亿次. 24900 亿用科学记数法表示为
12. 在函数 的图象上有两点 、, 当 , 且图象上有三点 , 则函数值 的大小关系为
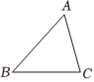
13. 在锐角
中,
, 在
内有一点
, 当
的和最小时,
的面积为
三、解答题 (共 13 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
14. 计算: .
15. 解不等式组
, 并把其解焦表示在数轴上.
16. 化简: .
17. 如图, 已知锐角
, 请用尺规作图法, 在
内部求作一点
, 使
,且
. (保留作图痕迹, 不写作法)
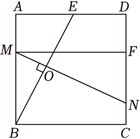
18. 如图, 在正方形
中,
为
上一点, 连接
是
上一点, 过点
作
于点
, 交
于点
, 过点
作
于点
. 求证:
.
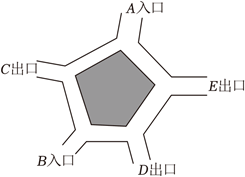
19. 清明节假期, 明明和亮亮约好参观展览馆, 如图是该展览馆出入口示意图. 明明和亮亮随机从两入口进入参观.
(1) 参观前, 明明从
入口进入的概率是
(2) 参观结束后, 通过画树状图或列表求明明和亮亮恰好从同一出口走出的概率.
20. 根据经营情况, 公司对某商品在甲、乙两地的销售单价进行了如下调整: 甲地上涨 , 乙地降价 5 元. 已知销售单价调整前甲地比乙地少 10 元, 调整后甲地比乙地少 1 元, 求调整前甲、乙两地该商品的销售单价.
21. 如图 1, 是某款手机支架摆放手机时的侧面示意图, 数学学习小组想要测量此支架的最高点到桌面的高度, 他们绘制了图 2 所示的侧面的截面图. 现测得支撑板
,
, 底座四边形
为矩形,
. 求手机支架最高点
到桌面
的距离. (结果精确到
, 参考数据:
)

22. 甲、乙两个工程组同时挖掘沈白高铁某段隧道, 两组每天挖掘长度均保持不变, 合作一段时间后, 乙组因维修设备而停工, 甲组单独完成了剩下的任务, 甲、乙两组挖掘的长度之和
与甲组挖掘时间
(天)之间的关系如图所示.
(1) 甲组比乙组多挖掘了 ________ 天.
(2) 求乙组停工后
关于
的函数解析式, 并写出自变量
的取值范围.
(3) 当甲组挖掘的总长度与乙组挖掘的总长度相等时, 直接写出乙组已停工的天数.

23. 某校为了解七八年级学生对卫生安全知识的掌握情况, 从七、八年级抽取 20 名学生进行测试, 并对成绩(百分制)进行收集、整理和分析.部分信息如下:收集数据:
七年级: 99 90 92 85 80 67 83 87 87 79 56 87 85 84 68 66 62 60 76 59
八年级: 97 95 80 96 88 79 92 78 86 83 86 86 75 72 60 77 78 76 58 65
整玾数据.

分析数据:
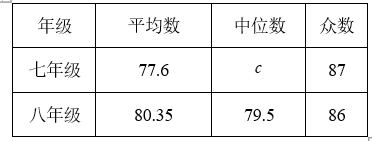
请根据以上信息, 回答下列问题:
(1) 填空:
,
(2) 补全频数分布直方图.
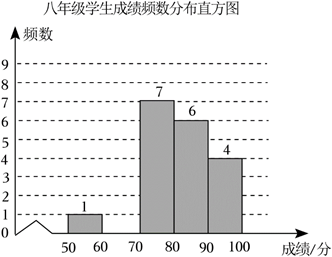
(3) 若该校七年级学生共有 1300 人, 假设全部参加此次测试, 请估计七年级测试成绩超过平均数 77.6 分的人数.
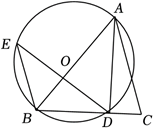
24. 如图, 在以
为直径的 圆
中, 点
在
上, 连接
, 过点
作
交
的延长线于点
.
(1) 求证:
;
(2) 若
, 求
的长.
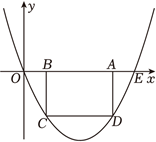
25. 如图, 抛物线过点
, 矩形
的边
在线段
上 (点
在点
的左
侧), 点
在抛物线上. 设
, 当
时,
.
(1) 求抛物线的函数表达式;
(2) 当
为何值时, 矩形
的周长有最大值? 最大值是多少?
(3) 保持
时的矩形
不动, 向右平移抛物线, 当平移后的抛物线与矩形的边有两个交点
, 且直线
平分矩形
的面积时, 求抛物线平移的距离.
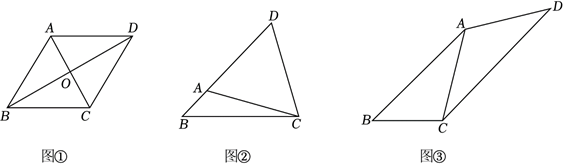
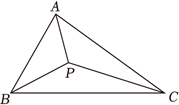
26. 【问题提出】
(1) 如图①, 在平行四边形
中, 对角线
、 相交于点
, 若
, 则
的面积为
【问题探究】
(2) 如图②, 已知
, 点
为
上方的一个动点, 且
, 点
为
延长线上一点, 且
, 连接
, 求
面积的最大值;
【问题解决】
(3) 如图③, 工人师傅需要制作一个四边形的模具, 在四边形
中, 要求
,
. 现要求四边形
的面积最大, 如果存在, 求出四边形
的最大面积, 如果不存在, 请说明理由. (结果保留根号)