【问题提出】
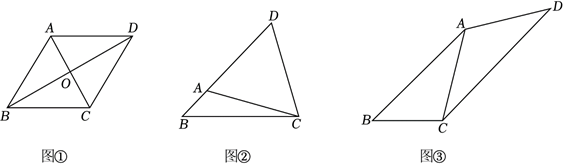
(1) 如图①, 在平行四边形 $A B C D$ 中, 对角线 $A C 、 B D$ 相交于点 $O$, 若 $S_{\triangle A B C}=5$, 则 $\triangle B C D$的面积为 $\qquad$
【问题探究】
(2) 如图②, 已知 $B C=12$, 点 $A$ 为 $B C$ 上方的一个动点, 且 $\angle B A C=120^{\circ}$, 点 $D$ 为 $B A$ 延长线上一点, 且 $A D=A C$, 连接 $C D$, 求 $\triangle B C D$ 面积的最大值;

【问题解决】
(3) 如图③, 工人师傅需要制作一个四边形的模具, 在四边形 $A B C D$ 中, 要求 $\angle B A C=30^{\circ}$, $B C=2 m, \angle C A D=120^{\circ}, A D=A C$. 现要求四边形 $A B C D$ 的面积最大, 如果存在, 求出四边形 $A B C D$ 的最大面积, 如果不存在, 请说明理由. (结果保留根号)