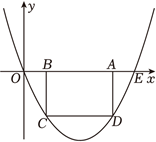
如图, 抛物线过点 $O(0,0), E(10,0)$, 矩形 $A B C D$ 的边 $A B$ 在线段 $O E$ 上 (点 $B$ 在点 $A$ 的左
侧), 点 $C, D$ 在抛物线上. 设 $B(t, 0)$, 当 $t=2$ 时, $B C=4$.
(1) 求抛物线的函数表达式;
(2) 当 $t$ 为何值时, 矩形 $A B C D$ 的周长有最大值? 最大值是多少?
(3) 保持 $t=2$ 时的矩形 $A B C D$ 不动, 向右平移抛物线, 当平移后的抛物线与矩形的边有两个交点 $G, H$, 且直线 $G H$ 平分矩形 $A B C D$ 的面积时, 求抛物线平移的距离.