单选题 (共 8 题 ),每题只有一个选项正确
已知等差数列 $\left\{a_n\right\}$ 前 15 项和为 45 , 若 $a_3=-10$, 则 $a_{13}=$
$\text{A.}$ 16
$\text{B.}$ 55
$\text{C.}$ -16
$\text{D.}$ 35
设 $f(x)$ 在 $x=x_0$ 处可导, 则 $\left.\lim _{\Delta x \rightarrow 0} \frac{f\left(x_0+\Delta x\right)-f\left(x_0\right)}{2 \Delta x}=\right.$
$\text{A.}$ $\frac{1}{2} f^{\prime}\left(x_0\right)$
$\text{B.}$ $2 f^{\prime}\left(-x_0\right)$
$\text{C.}$ $f^{\prime}\left(x_0\right)$
$\text{D.}$ $2 f^{\prime}\left(x_0\right)$
已知等比数列 $\left\{a_n\right\}$, 且 $a_1=1, a_5=5$, 则 $a_3$ 的值为
$\text{A.}$ 3
$\text{B.}$ $\sqrt{5}$
$\text{C.}$ $\pm \sqrt{5}$
$\text{D.}$ $\frac{5}{2}$
已知数列 $\left\{a_n\right\}$ 满足 $a_1=0, a_{n+1}=\frac{a_n-\sqrt{3}}{\sqrt{3} a_n+1}\left(n \in \mathbf{N}^*\right)$, 则 $a_{20}=$
$\text{A.}$ 0
$\text{B.}$ $-\sqrt{3}$
$\text{C.}$ $\sqrt{3}$
$\text{D.}$ $\frac{\sqrt{3}}{2}$
设函数 $f(x)=x^2-\frac{1}{2}, f^{\prime}(x)$ 是 $f(x)$ 的导数, 则函数 $g(x)=f^{\prime}$ ( $x) \cos x$ 的部分图象可以为
$\text{A.}$  $\text{B.}$
$\text{B.}$  $\text{C.}$
$\text{C.}$  $\text{D.}$
$\text{D.}$ 
5 名同学到 3 个小区参加垃圾分类宣传活动, 每名同学只去 1 小区, 每个小区至少安排 1 名同学, 则不同的安排方法共有
$\text{A.}$ 60 种
$\text{B.}$ 90 种
$\text{C.}$ 150 种
$\text{D.}$ 240 种
定义 $\frac{n}{p_1+p_2+\cdots+p_n}$ 为 $n$ 个正数 $p_1, p_2, \cdots, p_n$ 的 “均倒数”,已知数 $\left\{a_n\right\}$ 的前 $n$ 项的 “均倒数” 为 $\frac{1}{3 n+1}$, 又 $b_n=\frac{a_n+2}{6}$, 则 $\frac{1}{b_1 b_2}+\frac{1}{b_2 b_3}$ $\cdots+\frac{1}{b_9 b_{10}}=$
$\text{A.}$ $\frac{1}{11}$
$\text{B.}$ $\frac{10}{11}$
$\text{C.}$ $\frac{11}{12}$
$\text{D.}$ $\frac{9}{10}$
已知函数 $f(x)=\left\{\begin{array}{l}x^2+4 x+2, x \leqslant 0 \\ \frac{e \ln x}{x}, x>0\end{array}\right.$, 若函数 $g(x)=f(x)-$ $3 m$ 有 4 个不同的零点, 则 $m$ 的取值范围是
$\text{A.}$ $\left(0, \frac{2}{3}\right)$
$\text{B.}$ $\left(-\frac{2}{3}, \frac{2}{3}\right)$
$\text{C.}$ $\left(0, \frac{1}{3}\right)$
$\text{D.}$ $\left(-\frac{2}{3}, \frac{1}{3}\right)$
多选题 (共 4 题 ),每题有多个选项正确
下列选项正确的是
$\text{A.}$ $y=\ln 2$, 则 $y^{\prime}=\frac{1}{2}$
$\text{B.}$ $f(x)=\frac{1}{x^2}$, 则 $f^{\prime}(3)=-\frac{2}{27}$
$\text{C.}$ $\left(x^3 \mathrm{e}^x\right)^{\prime}=3 x^2 \mathrm{e}^x+x^3 \mathrm{e}^x$
$\text{D.}$ $\left(\frac{2 \sin x}{x^2}\right)^{\prime}=\frac{2 \cos x}{2 x}$
关于 $\left(\frac{1}{x}-2 x\right)^7$ 的二项展开式, 下列说法正确的是
$\text{A.}$ 二项式系数和为 128
$\text{B.}$ 各项系数和为 -7
$\text{C.}$ $x^{-1}$ 项的系数为 -280
$\text{D.}$ 第三项和第四项的系数相等
设等差数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 公差为 $d$. 已知 $a_3=12$, $S_{12}>0, a_7 < 0$, 则
$\text{A.}$ $a_6>0$
$\text{B.}$ $-\frac{24}{7} < d < -3$
$\text{C.}$ $S_n < 0$ 时, $n$ 的最小值为 14
$\text{D.}$ 数列 $\left\{\frac{S_n}{a_n}\right\}$ 中最小项为第 7 项
已知函数 $f(x)$ 满足 $x f^{\prime}(x)+f(x)=\ln x+1, f(1)=2$, 则当 $x$ $>0$ 时,下列说法正确的是
$\text{A.}$ $f(2)=\ln 2+1$
$\text{B.}$ $x = 2$ 是函数$ f(x)$ 的极大值点
$\text{C.}$ 函数$y = f(x) - x $有且只有一个零点
$\text{D.}$ 存在正实数 $k$, 使得 $f(x)>k x$ 恒成立
填空题 (共 2 题 ),请把答案直接填写在答题纸上
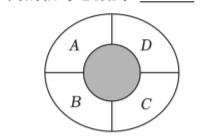
如图,一圆形信号灯分成 A,B,C,D 四块灯带区域,现有 4种不同的颜色供灯带使用,要求在每块灯带里选择 1 种颜色,且相邻的 2 块灯带选择不同的颜色,则不同的信号总数为
已知数列 $\left\{a_n\right\}$ 满足 $a_n=\left\{\begin{array}{l}1, n=1 \\ \log _n(n+1), n \geqslant 2, n \in \mathbf{N}^*\end{array}\right.$, 定义使 $a_1 \cdot a_2 \cdot a_3 \cdots \cdots \cdot a_k\left(k \in \mathbf{N}^*\right)$ 为整数的 $k$ 叫做 “幸福数”, 则区间 $[1,2022]$ 内所有 “幸福数” 的和为
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
$S_n$ 为等差数列 $\left\{a_n\right\}$ 的前 $n$ 项和, 已知 $a_7=1, S_4=-32$.
(1) 求数列 $\left\{a_n\right\}$ 的通项公式.
(2) 求 $S_n$, 并求 $S_n$ 的最小值.
设 $x=-3$ 是函数 $f(x)=a x^3+b x^2-3 x+c$ 的一个极值点, 曲线 $y=f(x)$ 在 $x=1$ 处的切线斜率为 8 .
(1) 求 $f(x)$ 的单调区间;
(2) 若 $f(x)$ 在闭区间 $[-1,1]$ 上的最大值为 10 , 求 $c$ 的值.
(1) 高二 (10) 班元旦晚会有 2 个唱歌节目 $a$ 和 $b ; 2$ 个相声节目 $c$ 和 $d$. 要求排出一个节目单, 满足第一个节目和最后一个节目都是唱歌节目. 列出所有可能的排列.
(2) 甲乙丙丁戊已庚 7 个人排成一排拍照片, 若要求甲、乙、丙 3 人必须相邻, 并且丁和戊不相邻, 有多少种不同排法? (结果用数字表示)
(3) 从 4 名男教师和 5 名女教师中选出 4 名教师参加新教材培训, 要求有男有女且至少有 2 名男教师参加, 有多少种不同的选法? (结果用数字表示)
已知数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 当 $n \in \mathbf{N}^*$ 时, $S_n+2=2 a_n$;数列 $\left\{b_n\right\}$ 中, $b_1=1$. 直线 $x-y+1=0$ 经过点 $P\left(b_n, b_{n+1}\right)$.
(1) 求数列 $\left\{a_n\right\} 、\left\{b_n\right\}$ 的通项公式 $a_n$ 和 $b_n$;
(2) 设 $c_n=a_n b_n$, 求数列 $\left\{c_n\right\}$ 前 $n$ 项和 $T_n$, 并求 $T_n < 2022$ 的最大整数 $n$.
设函数 $f(x)=\mathrm{e}^x-a x-2$.
(1) 求 $f(x)$ 的单调区间;
(2) 若 $a=1$ 且当 $x>0$ 时 $(x-k) f^{\prime}(x)+x+1>0$, 求整数 $k$ 的最大值.