单选题 (共 10 题 ),每题只有一个选项正确
如图, 在 $\triangle A B C$ 中, $\angle C D E=64^{\circ}, \angle A=28^{\circ}, D E$ 垂直平分 $B C$, 则 $\angle A B D=$

$\text{A.}$ $100^{\circ}$
$\text{B.}$ $128^{\circ}$
$\text{C.}$ $108^{\circ}$
$\text{D.}$ $98^{\circ}$
如图, $\triangle A B C$ 的外角平分线 $B D, C E$ 相交于点 $P$. 若点 $P$ 到 $A C$ 的距离为 3 , 则点 $P$ 到 $A B$ 的距离为

$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
如图, 在 $\triangle A B C$ 中, $\angle B=30^{\circ}, \angle C=45^{\circ}, A D$ 平分 $\angle B A C$ 交 $B C$ 于 点 $D, D E \perp A B$, 垂足为 $E$. 若 $D E=1$, 则 $B C$ 的长为

$\text{A.}$ $2+\sqrt{2}$
$\text{B.}$ $\sqrt{2}+\sqrt{3}$
$\text{C.}$ $2+\sqrt{3}$
$\text{D.}$ $3$
已知直角三角形两条直角边的边长之和为 $\sqrt{6}$, 斜边长为 2 , 则这个三角形的面积是
$\text{A.}$ $0.25$
$\text{B.}$ $0.5$
$\text{C.}$ $1$
$\text{D.}$ $2 \sqrt{3}$
到三角形三个顶点距离相等的是
$\text{A.}$ 三条中线交点
$\text{B.}$ 三条高的交点
$\text{C.}$ 三条角平分线的交点
$\text{D.}$ 三条中垂线的交点
某次知识竞赛共 20 道题, 每答对一道题得 10 分, 答错或不答都扣 5 分, 娜娜得分超过了 90 分. 设她答对了 $x$ 道题, 则根据题意可列不等式为
$\text{A.}$ $10 x-5(20-x) \geq 90$
$\text{B.}$ $10 x-5(20-x)>90$
$\text{C.}$ $20 \times 10-5 x>90$
$\text{D.}$ $20 \times 10-5 x \geq 90$
下列推理正确的是
$\text{A.}$ 因为 $a < b$, 所以 $a+2 < b+1$
$\text{B.}$ 因为 $a < b$, 所以 $a-1 < b-2$
$\text{C.}$ 因为 $a>b$, 所以 $a+c>b+c$
$\text{D.}$ 因为 $a>b$, 所以 $a+c>b-d$
已知关于 $x$ 的不等式 $x-a < 1$ 的解如图所示, 则 $a$ 的取值是

$\text{A.}$ 0
$\text{B.}$ 1
$\text{C.}$ 2
$\text{D.}$ 3
有一根 $40 \mathrm{~cm}$ 的金属棒, 欲将其截成 $x$ 根 $7 \mathrm{~cm}$ 的小段和 $y$ 根 $9 \mathrm{~cm}$ 的小段, 剩余部分作废料处 理, 若使废料最少, 则正整数 $x, y$ 应分别为
$\text{A.}$ $x=1, y=3$
$\text{B.}$ $x=4, y=1$
$\text{C.}$ $x=3, y=2$
$\text{D.}$ $x=2, y=3$
如图, 射线 $O A$ 是第三象限的角平分线, 若点 $B(k-3,1-2 k)$ 在第三象限 内.且在射线 $O A$ 的下方, 则 $k$ 的取值范围是

$\text{A.}$ $k < \frac{1}{2}$
$\text{B.}$ $\frac{1}{2} < k < 3$
$\text{C.}$ $\frac{1}{2} < k < \frac{4}{3}$
$\text{D.}$ $\frac{4}{3} < k < 3$
填空题 (共 5 题 ),请把答案直接填写在答题纸上
如图, 在一次暴风灾害中, 一棵大树在离地面 2 米处折断, 树的另一部 分倒地后与地面成 $30^{\circ}$ 角, 那么这棵树折断之前的高度是 ( ) 米.

如图, 在 $\triangle A B C$ 中, $A B=A C=4, \angle B=\angle C=15^{\circ}$, 则 $\triangle A B C$ 的面积为

三个等边三角形的摆放位置如图所示, 若 $\angle 1+\angle 2=120^{\circ}$, 则 $\angle 3$ 的度数
为

某次知识竞赛共有 20 道题, 每答对一题得 10 分, 答错或不答都扣 5 分, 娜娜得分要超过 90 分, 设她答对了 $n$ 道题, 则根据题意可列不等式为
已知 $x, y, z$ 为非负数, 满足 $\left\{\begin{array}{c}x+y+z=30 \\ 2 x+3 y+4 z=100\end{array}\right.$, 设 $s=3 x+2 y+5 z$, 则 $s$ 的取值范围是
解答题 (共 10 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
解不等式: $\frac{x-2}{2} \leq \frac{7-x}{3}$.
解不等式组 $\left\{\begin{array}{l}\frac{1}{2} x+1 < 7-\frac{3}{2} x \\ \frac{3 x-2}{3} \geq \frac{x}{3}+\frac{x-4}{4} \end{array}\right.$ 并与出它的所有整数解.
(1)如图①, 点 $D, E$ 分别在等边 $\triangle \mathrm{ABC}$ 的边 $B C, A B$ 上, 且 $\mathrm{AE}=\mathrm{BD}$, 连接 $A D$, $C E$ 交于点 $F$. 找出图中与 $\triangle \mathrm{ABD}$ 全等的三角形, 证明并求出 $\angle \mathrm{AFE}$ 的度数;
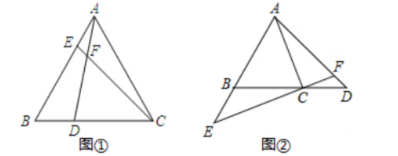
(2) 如图②, 若(1) 中的点 $D, E$ 分别在等边 $\triangle \mathrm{ABC}$ 的边 $B C, A B$ 延长线上, (1)中的结论是否仍然成立? 请说明理由.
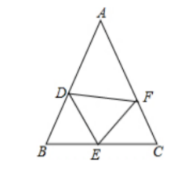
如图, $\triangle \mathrm{ABC}$ 中, $\mathrm{AB}=\mathrm{AC}, D, E, F$ 分别为 $A B, B C, C A$ 上的点, 且 $\mathrm{BD}=\mathrm{CE}$,
$\angle \mathrm{DEF}=\angle B$
(1)求证: $\triangle \mathrm{BDE} \cong \triangle \mathrm{CEF}$;
(2) 若 $\angle A=40^{\circ}$, 求 $\angle E D F$ 的度数.
如图, 四边形 $A B C D$ 中, $\angle B=90^{\circ}, A B / / C D, M$ 为 $B C$ 边上的一点, 且 $A M$ 平分 $\angle B A D, D M$ 平分 $\angle A D C$.
(1)求证: $A M \perp D M$;
(2) 若 $B C=8$, 求点 $M$ 到 $A D$ 的距离.

我市在创建全国文明城市过程中, 决定购买 $A, B$ 两种树苗对某路段道路进行绿化 改造, 已知购买 $A$ 种树苗 8 棵, $B$ 种树苗 3 棵, 需要 950 元; 若购买 $A$ 种树苗 5 棵, $B$ 种树 苗 6 棵, 则需要 800 元.
(1)求 $A, B$ 两种树苗每棵各多少元?
(2)考虑到绿化效果和资金周转, 购进 $A$ 种树苗不能少于 52 棵, 且用于财买这两种树苗的资 金不能超过 7650 元, 若购进这两种树苗共 100 棵, 则有哪几种购买方案?
(3)某包工队承包种植任务, 若种好一棵 $A$ 种树苗可获工钱 30 元, 种好一棵 $B$ 种树苗可获工 钱 20 元, 在第(2)问的购买方案中, 种好这 100 棵树苗, 哪一种购买方案所付的种植工钱最 少? 最少工钱是多少元?
下列变形是怎样得到的?
(1) 由 $\frac{1}{2} x-3>\frac{1}{2} y-3$, 得 $x>y$;
(2) 由 $\frac{1}{2}(x-3)>\frac{1}{2}(y-3)$, 得 $x>y$;
(3)由 $2(3-x) < 2(3-y)$, 得 $x>y$.
如图, 已知等腰三角形 $A B C$ 中, $A B=A C$, 点 $D 、 E$ 分别在边 $A B 、 A C$ 上, 且 $A D=A E$, 连接 $B E 、 C D$, 交于点 $F$.
(1)判断 $\angle A B E$ 与 $\angle A C D$ 的数量关系, 并说明理由;
(2)求证:过点 $A 、 F$ 的直线垂直平分线段 $B C$.

一家科技公司准备生产甲、乙两种商品共 8 万件销往 “一带一路” 沿线国家和地 区. 已知 2 件甲种商品与 3 件乙种商品的销售收入相同, 3 件甲种商品比 2 件乙种商品的销 售收入多 1500 元.
(1)甲种商品与乙种商品的销售单价各是多少元?
(2)若甲、乙两种商品的销售总收入不低于 5400 万元, 则至少销售甲种商品多少万件?
今年 6 月以来, 我国多地遭遇强降雨, 引发洪涝灾害, 人民的生活受到了极大的影 响. “一方有难, 八方支援”, 某市筹集了大量的生活物资, 用 $A, B$ 两种型号的货车, 分 两批运往受灾严重的地区. 具体运输情况如下:

备注: 第一批、第二批每辆货车均满载
(1) 求 $A, B$ 两种型号货车每辆满载分别能运多少吨生活物资?
(2)该市后续又筹集了 $62.4$ 吨生活物资, 现已联系了 3 辆 $A$ 种型号货车. 试问至少还需联系 多少辆 $B$ 种型号货车才能一次性将这批生活物资运往目的地?