单选题 (共 8 题 ),每题只有一个选项正确
设集合 $A$ 和 $B$ 都是自然数集合 $N$ ,映射 $f: A \rightarrow B$ 把集合 $A$ 中的元素 $n$ 映射到集合 $B$ 中的元素 $2^n+n$, 则在映射 $f$ 下, 象 20 的原象是
$\text{A.}$ 2
$\text{B.}$ 3
$\text{C.}$ 4
$\text{D.}$ 5
在复平面内,把复数 $3-\sqrt{3 i}$ 对应的向量按顺时针方向旋转 $\frac{\pi}{3}$ ,所得向量对应的复数是
$\text{A.}$ $2 \sqrt{3}$
$\text{B.}$ $-2 \sqrt{3 i}$
$\text{C.}$ $\sqrt{3}-3 {i}$
$\text{D.}$ $3+\sqrt{3 i}$
一个长方体共一顶点的三个面的面积分别是 $\sqrt{2}, \sqrt{3} \sqrt{6}$, 这个长方体对角线的长是
$\text{A.}$ $2 \sqrt{3}$
$\text{B.}$ $3 \sqrt{2}$
$\text{C.}$ 6
$\text{D.}$ $\sqrt{6}$
已知 $\sin \alpha>\sin \beta$, 那么下列命题成立的是
$\text{A.}$ 若 $\alpha 、 \beta$ 是第一象限角, 则 $\cos \alpha>\cos \beta$
$\text{B.}$ 若 $\alpha 、 \beta$ 是第二象限角, 则 $\operatorname{tg} \alpha>\operatorname{tg} \beta$
$\text{C.}$ 若 $\alpha$ 、 $\beta$ 是第三象限角, 则 $\cos \alpha>\cos \beta$
$\text{D.}$ 若 $\alpha 、 \beta$ 是第四象限角, 则 $\operatorname{tg} \alpha>\operatorname{tg} \beta$
函数 $y=-x \cos x$ 的部分图象是
$\text{A.}$ 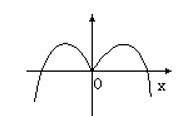 $\text{B.}$
$\text{B.}$ 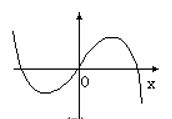 $\text{C.}$
$\text{C.}$ 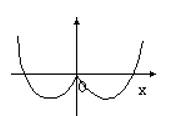 $\text{D.}$
$\text{D.}$ 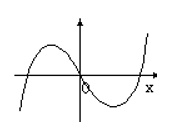
若 $a>b>1, P=\sqrt{\lg a \cdot \lg b}, Q=\frac{1}{2}(\lg a+\lg b), R=\lg \left(\frac{a+b}{2}\right)$, 则
$\text{A.}$ $\mathrm{R} < \mathrm{P} < \mathrm{Q}$
$\text{B.}$ $\mathrm{P} < \mathrm{Q} < \mathrm{R}$
$\text{C.}$ $\mathrm{Q} < \mathrm{P} < \mathrm{R}$
$\text{D.}$ $\mathrm{P} < \mathrm{R} < \mathrm{Q}$
过原点的直线与圆 $x^2+y^2+4 x+3=0$ 相切, 若切点在第三象限, 则该直线的方程是
$\text{A.}$ $y=\sqrt{3} x$
$\text{B.}$ ${y}=-\sqrt{3} {x}$
$\text{C.}$ ${y}=\frac{\sqrt{3}}{3} {x}$
$\text{D.}$ $y=-\frac{\sqrt{3}}{3} x$
过抛物线 ${y}={ax}^2(a>0)$ 的焦点 $F$ 作一直线交抛物线于 $P 、 Q$ 两点, 若线段 $P F$ 与 $F Q$的长分别是 $p 、 q$, 则 $\frac{1}{p}+\frac{1}{q}$ 等于
$\text{A.}$ $2 a$
$\text{B.}$ $\frac{1}{2 {a}}$
$\text{C.}$ $4 a$
$\text{D.}$ $\frac{4}{a}$
填空题 (共 1 题 ),请把答案直接填写在答题纸上
设 ${\left\{a_n\right\}}$ 是首项为 1 的正项数列, 且 ${(n+1) a_{n+1}^2-n a_n^2+a_{n+1} a_n=0}(n=1,2,3 \cdots)$,则它的通项公式是 $\mathrm{a}_{\mathrm{n}}=$ $\qquad$
解答题 (共 2 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知函数 $y=\frac{1}{2} \cos ^2 x+\frac{\sqrt{3}}{2} \sin x \cos x+1, x \in R$
(I) 当函数 y 取得最大值时, 求自变量 x 的集合;
(II) 该函数的图象可由 $y=\sin x(x \in R)$ 的图象经过怎样的平移和伸缩变换得到?
设函数 ${f}({x})=\sqrt{{x}^2+1}-{ax}$ ,其中 ${a}>0$ 。
(I) 解不等式 $f(x) \leqslant 1$;
(II) 求 a 的取值范围, 使函数 $f(x)$ 在区间 $[0,+\infty]$ 上是单调函数。