单选题 (共 4 题 ),每题只有一个选项正确
已知实数 $a, b, c$ 满足 $2 a+13 b+3 c=90,3 a+9 b+c=72$, 则 $\frac{3 b+c}{a+2 b}=$
$\text{A.}$ 2
$\text{B.}$ 1
$\text{C.}$ 0
$\text{D.}$ -1
若正整数 $a, b, c$ 满足 $a \leq b \leq c$ 且 $a b c=2(a+b+c)$, 则称 $(a, b, c)$ 为好数组. 那么, 好数组的个数为
$\text{A.}$ 1个
$\text{B.}$ 2个
$\text{C.}$ 3个
$\text{D.}$ 4个
对于正整数 $n$, 设 $a_n$ 是最接近 $n$ 的整数, 则 $\frac{1}{a_1}+\frac{1}{a_2}+\cdots+\frac{1}{a_n}=$
$\text{A.}$ $\frac{191}{7}$.
$\text{B.}$ $\frac{192}{7}$.
$\text{C.}$ $\frac{193}{7}$.
$\text{D.}$ $\frac{194}{7}$.
设 $A$ 是以 $B C$ 为直径的圆上的一点, $A D \perp B C$ 于点 $D$, 点 $E$ 在线段 $D C$ 上, 点 $F$ 在 $C B$ 的延长线上,满足 $\angle B A F=\angle C A E$. 已知 $B C=15, B F=6, B D=3$, 则 $A E=$
$\text{A.}$ $4 \sqrt{3}$.
$\text{B.}$ $2 \sqrt{13}$.
$\text{C.}$ $2 \sqrt{14}$.
$\text{D.}$ $2 \sqrt{15}$.
填空题 (共 4 题 ),请把答案直接填写在答题纸上
使得等式 $\sqrt{1+\sqrt{1+a}}=\sqrt[3]{a}$ 成立的实数 $a$ 的值为
若实数 $x, y$ 满足 $x^3+y^3+3 x y=1$, 则 $x^2+y^2$ 的最小值为
设 $m, n$ 是正整数, 且 $m>n$. 若 $9^m$ 与 $9^n$ 的末两位数字相同, 则 $m-n$ 的最小值为
已知正整数 $a, b, c$ 满足 $2 a^2-6 b x-3 c+9=0,-6 a+b^2+c=0$, 则 $a^2+b^2+c^2=$
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知实数 $x, y$ 满足 $x+y=3, \frac{1}{x+y^2}+\frac{1}{x^2+y}=\frac{1}{2}$, 求 $x^5+y^5$ 的值.
已知实数 $a, b, c$ 满足 $a \leq b \leq c, a+b+c=16, a^2+b^2+c^2+\frac{1}{4} a b c=128$,求 $c$ 的值.
求所有的正整数 $m$, 使得 $2^{2 m-1}-2^m+1$ 是完全平方数.
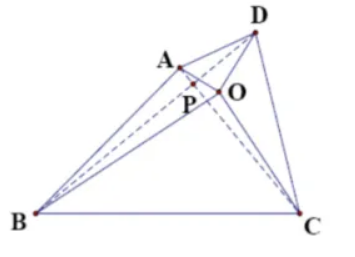
如图, $O$ 为四边形 $A B C D$ 内一点, $\angle O A D=\angle O C B, O A \perp O D, O B \perp O C$.求证: $A B^2+C D^2=A D^2+B C^2$.
求所有的正整数数对 $(a, b)$, 使得 $a^3=49 \times 3^b+8$
若 $a^2=a+1 , b^2=b+1 (a \ne b)$, 求 $a^2+b^2$的值