解答题 (共 10 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
设一批电子产品由甲和乙两工厂共同生产, 其中甲, 乙两工厂生产的份额分别为 $60 \%$ 和 $40 \%$ 。根据经验可知甲, 乙两工厂生产该产品的次品率分别为 $1 \%$ 和 $2 \%$, 现从这批产品中随机抽取一件, 发现是次品, 则该次品是甲厂生产的概率是多少?
设某保险公司每个月受理的索赔事件个数服从参数为 $\lambda$ 的Poisson分布, 而每个索赔成功的概率为 $p$, 且各个索赔彼此之间没有关系。二月份该公司有 $k$ 个索赔成功的概率是多少? 若该月份有 $k$ 个索赔成功, 则它受理了 $m(m \geq k)$ 个索赔事件的概率是多少?
设 $X$ 的概率密度函数为 $f(x)=(1+\theta) x^\theta, 0 < x < 1$. 现考虑假设检验问题 $H_0: \theta=5 \leftrightarrow H_1: \theta=3$. 该检验的否定域为 $X>1 / 2$, 则犯第一类错误的概率和第二类错误的概率分别为多少?
已知一批零件的长度 $X$ (单位: $\mathrm{cm}$ )服从正态分布 $N(\mu, 1)$, 从中随机抽取 16 个零件, 得到长度的平均值为 $40 \mathrm{~cm}$, 试求 $\mu$ 的置信水平为 0.95 的置信区间?
设 $X_1, \ldots, X_n$ 是来自总体 $X$ 的独立同分布样本, 且都只取正值, 试求数学期望:
$$
E\left(\frac{X_1}{\sum_{i=1}^n X_i}\right) .
$$
某工厂为了保证设备正常工作, 需配备适量的维修工人(工人配备多了就浪费, 配备少了又要影响生产), 现有同类型设备 300 台, 各台工作是相互独立的, 发生故障的概率都是 0.01 . 在通常情况下一台设备的故障可由一个人来处理(我们也只考虑这种情况), 问至少需配备多少工人, 才能保证设备发生故障但不能及时维修的概率小于 0.01 ?
设随机向量 $(\xi, \eta)$ 服从区域 $D$ 上的均匀分布, 其中 $D$ 是由直线 $y=x, x=0, y=$ 1所围成的区域. 试求:
(1) $(\xi, \eta)$ 的联合密度 $p(x, y)$;
(2) $(\xi, \eta)$ 的边缘密度 $p_1(x)$ 和 $p_2(y)$;
(3) 条件密度 $p(x \mid \eta=y)$;
(4) $E(\xi \mid \eta=y)$.
设总体 $X$ 的概率分布如下表, 其中 $0 < \theta < 1$ 为未知参数. 现从此总体中随机抽取 100 个样本, 发现有 17 个样本取值为 0,33 个样本取值为 1,50 个样本取值为 2 .
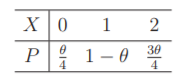
(1) 求 $\theta$ 的矩估计 $\hat{\theta}_1$ 和极大似然估计 $\hat{\theta}_2$; 并分别计算相应的估计值。
(2) $\hat{\theta}_1$ 和 $\hat{\theta}_2$ 是否是无偏的? 若否, 请修正。
(3) 请问修正后的估计那个更有效?
简. 奥斯汀 (1775 - 1817), 英国女作家, 作品有: 《理智与情感》, 《傲慢与偏见》, 《爱玛》等, 在其身后, 她的哥哥亨利主持了遗作《劝导》和《诺桑觉寺》两部作品出版。下面表格收集了代表作《理智与情感》, 《爱玛》以及《劝导》前两章中常用代表词的出现频数,
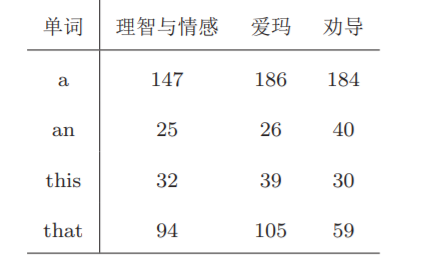
请问作品《理智与情感》, 《爱玛》以及《劝导》之间在选择常用词比例是否存在差异? $(\alpha=0.05)$
为比较甲和乙两处矿石的含灰率(\%), 分别从甲、乙两处随机抽取矿石6块, 甲处矿石含灰率数据是: $17,14,18,13,19$ 和 15 ; 而乙处矿石含灰率数据为: $16,19,20$, 22,18 和 19 . 假设两处矿石含灰率分别服从正态分布, 且总体独立, 均值和方差未知.试根据以上数据判断:
(1)(6 分) 在显著水平 0.05 下, 甲、乙两处矿石含灰率的方差是否相等?
(2)(9 分) 在显著水平 0.05 下, 乙处矿石含灰率的平均量是否显著地高于甲处矿石含灰率的平均量?
附录 分位数: $u_{0.025}=1.960, u_{0.05}=1.645, t_{0.025}(10)=2.228, t_{0.05}(10)=1.812, t_{0.025}(11)=$ $2.201, t_{0.05}(11)=1.796, t_{0.025}(12)=2.178, t_{0.05}(12)=1.782, \chi_{0.05}^2(1)=3.841, \chi_{0.05}^2(2)=$ $5.991, \chi_{0.05}^2(6)=12.591, F_{0.05}(5,5)=5.050, F_{0.025}(5,5)=7.146, F_{0.05}(6,6)=4.284$ $F_{0.025}(6,6)=5.820$.