单选题 (共 11 题 ),每题只有一个选项正确
下列说法中正确的是
$\text{A.}$ 若两个向量相等,则它们的起点和终点分别重合
$\text{B.}$ 模相等的两个平行向量是相等向量
$\text{C.}$ 若a和b都是单位向量,则a=b
$\text{D.}$ 零向量与其它向量都共线
化简 $\overrightarrow{A C}-\overrightarrow{B D}+\overrightarrow{C D}-\overrightarrow{A B}$ 得
$\text{A.}$ $\overrightarrow{0}$
$\text{B.}$ $\overrightarrow{D A}$
$\text{C.}$ $\overrightarrow{B C}$
$\text{D.}$ $\overrightarrow{A B}$
已知向量 $\vec{a}=(x-1,2), \vec{b}=(2,1)$, 则 $\vec{a} \perp \vec{b}$ 的充要条件是
$\text{A.}$ $x=-\frac{1}{2}$
$\text{B.}$ $x=-1$
$\text{C.}$ $x=5$
$\text{D.}$ $x=0$
若 $\overrightarrow{e_1}, \overrightarrow{e_2}$ 是平面 $\alpha$ 内的一组基底, 则下列四组向量能作为平面 $\alpha$ 的一组基底的是
$\text{A.}$ $\overrightarrow{e_1}-\overrightarrow{e_2}, \overrightarrow{e_2}-\overrightarrow{e_1}$
$\text{B.}$ $\overrightarrow{e_1}+\overrightarrow{e_2}, \overrightarrow{e_1}-\overrightarrow{e_2}$
$\text{C.}$ $2 \overrightarrow{e_2}-3 \overrightarrow{e_1},-6 \overrightarrow{e_1}+4 \overrightarrow{e_2}$
$\text{D.}$ $2 \overrightarrow{e_1}+\overrightarrow{e_2}, \overrightarrow{e_1}+\frac{1}{2} \overrightarrow{e_2}$
向量 $\overrightarrow{P A}=(k, 12), \overrightarrow{P B}=(4,5), \overrightarrow{P C}=(10, k)$, 若 $A, B, C$ 三点共线, 则 $k$ 的值为
$\text{A.}$ -2
$\text{B.}$ 11
$\text{C.}$ -2 或 11
$\text{D.}$ 2 或 11
下列关于向量 $\vec{a}, \vec{b}$, $\vec{c}$ 的运算, 不一定成立的是
$\text{A.}$ $(\vec{a}+\vec{b}) \cdot \vec{c}=\vec{a} \cdot \vec{c}+\vec{b} \cdot \vec{c}$
$\text{B.}$ $(\vec{a} \cdot \vec{b}) \cdot \vec{c}=\vec{a} \cdot(\vec{b} \cdot \vec{c})$
$\text{C.}$ $\vec{a} * \vec{b} \le | \vec{a}|* |\vec{b}|$
$\text{D.}$ $ | \vec{a} - \vec{b}| \le | \vec{a}| + | \vec{b}|$
已知两个非零向量 $\vec{a}, \vec{b}$ 满足 $|\vec{a}+\vec{b}|=|\vec{a}-\vec{b}|$, 则下面结论正确的是
$\text{A.}$ $\vec{a} / / \vec{b}$
$\text{B.}$ $\vec{a} \perp \vec{b}$
$\text{C.}$ $|\vec{a}|=|\vec{b}|$
$\text{D.}$ $\vec{a}+\vec{b}=\vec{a}-\vec{b}$
已知点 $A(3,-2), B(-5,-1)$, 且 $\overrightarrow{A P}=\frac{1}{2} \overrightarrow{A B}$, 则点 $P$ 的坐标为
$\text{A.}$ $\left(-1,-\frac{3}{2}\right)$
$\text{B.}$ $(-8,1)$
$\text{C.}$ $\left(1, \frac{3}{2}\right)$
$\text{D.}$ $(8,-1)$
已知向量 $\vec{a}, \vec{b}$ 满足 $|\vec{a}|=5,|\vec{b}|=6, \vec{a} \cdot \vec{b}=-6$, 则向量 $\vec{a}$ 和向量 $\vec{a}+\vec{b}$ 夹角的余弦值
$\text{A.}$ $-\frac{31}{35}$
$\text{B.}$ $-\frac{19}{35}$
$\text{C.}$ $\frac{17}{35}$
$\text{D.}$ $\frac{19}{35}$
如图, 在 $\triangle A B C$ 中, $\overrightarrow{A N}=\frac{1}{3} \overrightarrow{N C}, P$ 是 $B N$ 上的一点, 若 $\overrightarrow{A P}=m \overrightarrow{A B}+\frac{2}{11} \overrightarrow{A C}$, 则实数 $m$ 的值为
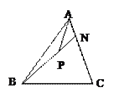
$\text{A.}$ $\frac{9}{11}$
$\text{B.}$ $\frac{5}{11}$
$\text{C.}$ $\frac{3}{11}$
$\text{D.}$ $\frac{2}{11}$
在日常生活中, 我们会看到如图所示的情境, 两个人共提一个行李包.假设行李包所受重力为 $\vec{G}$, 作用 在行李包上的两个拉力分别为 $\overrightarrow{F_1}, \overrightarrow{F_2}$, 且 $\left|\overrightarrow{F_1}\right|=\left|\overrightarrow{F_2}\right|, \overrightarrow{F_1}$ 与 $\overrightarrow{F_2}$ 的夹角为 $\theta$, 下列结论中正确的是

$\text{A.}$ $\theta$ 越小越费力, $\theta$ 越大越省力
$\text{B.}$ $\theta$ 的范围为 $[0, \pi]$
$\text{C.}$ 当 $\theta=\frac{\pi}{2}$ 时, $\left|\overrightarrow{F_1}\right|=|\vec{G}|$
$\text{D.}$ 当 $\theta=\frac{2 \pi}{3}$ 时, $\left|\overrightarrow{F_1}\right|=|\vec{G}| \mid$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
$3(2 \vec{a}-\vec{b})-5(\vec{a}+3 \vec{b})=$
已知点 $A, B, C$ 的坐标分别是 $(2,-4),(0,6),(-8,10)$, 则 $\overrightarrow{B C}-\frac{1}{2} \overrightarrow{A C}=$
已知向量 $\vec{a}, \vec{b}$ 夹角为 $45^{\circ}$, 且 $|\vec{a}|=1,|2 \vec{a}-\vec{b}|=\sqrt{10}$, 则 $|\vec{b}|=$
如图, 在矩形 $A B C D$ 中, $A B=\sqrt{2}, B C=2$, 点 $E$ 为 $B C$ 的中点, 点 $F$ 在边 $C D$ 上, 若 $\overrightarrow{A B} \cdot \overrightarrow{A F}=\sqrt{2}$, 则 $A E \cdot B F$ 的值是
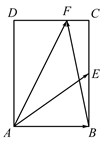
解答题 (共 1 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知 $|\vec{a}|=2,|\vec{b}|=1,(2 \vec{a}-3 \vec{b}) \cdot(2 \vec{a}+\vec{b})=17$.
(1) 求 $\vec{a}$ 与 $\vec{b}$ 的夹角;
(2) 若 $|\vec{a}+t \vec{b}|=2 \sqrt{3}$, 求实数 $t$ 的值;
(3) 设 $\vec{c}=m \vec{a}+2 \vec{b}, \vec{d}=2 \vec{a}-\vec{b}$, 若 $\vec{c}$ 与 $\vec{d}$ 共线, 求实数 $m$ 的值.