单选题 (共 8 题 ),每题只有一个选项正确
$\left(x+\frac{y^2}{x}\right)(x+y)^5$ 的展开式中 $x^3 y^3$ 的系数为
$\text{A.}$ 5
$\text{B.}$ 10
$\text{C.}$ 15
$\text{D.}$ 20
$22^{22}$ 除以 5 的余数是
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
已知 $n!=1 \times 2 \times 3 \times \mathrm{L} \times n$ ,则 $1!+2!+3!+\cdots+2022$ !被 5 除所得余数为
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
若 $(2 x+1)^{100}=a_0+a_1 x+a_2 x^2+\cdots+a_{100} x^{100}$ ,则 $2\left(a_1+a_3+\cdots+a_{99}\right)-3$ 被 8 整除的余数为
$\text{A.}$ 4
$\text{B.}$ 5
$\text{C.}$ 6
$\text{D.}$ 7
二项式定理,又称牛顿二项式定理,由艾萨克•牛顿提出.二项式定理可以推广到任意实数次幂,即广义二项式定理:
对于任意实数 $\alpha,(1+x)^\alpha=1+\frac{\alpha}{1!} \cdot x+\frac{\alpha(\alpha-1)}{2!} \cdot x^2+\cdots+\frac{\alpha(\alpha-1) \cdots(\alpha-k+1)}{k!} \cdot x^k+\cdots$
当 $|x|$ 比较小的时候,取广义二项式定理展开式的前两项可得:$(1+x)^a \approx 1+\alpha \cdot x$ ,并且 $|x|$ 的值越小,所得结果就越接近真实数据.用这个方法计算 $\sqrt{5}$ 的近似值,可以这样操作:
$$
\sqrt{5}=\sqrt{4+1}=\sqrt{4\left(1+\frac{1}{4}\right)}=2 \sqrt{1+\frac{1}{4}} \approx 2 \times\left(1+\frac{1}{2} \times \frac{1}{4}\right)=2.25 .
$$
用这样的方法,估计 $\sqrt[3]{25}$ 的近似值约为
$\text{A.}$ 2.922
$\text{B.}$ 2.926
$\text{C.}$ 2.928
$\text{D.}$ 2.930
已知 $(1-2 x)^{2021}=a_0+a_1 x+\cdots+a_{2021} x^{2021}$ ,则 $\frac{a_1}{2}+\frac{a_2}{2^2}+\frac{a_3}{2^3}+\cdots+\frac{a_{2021}}{2^{2021}}=$
$\text{A.}$ -2
$\text{B.}$ -1
$\text{C.}$ 0
$\text{D.}$ 2
我国南宋数学家杨辉 1261 年所著的《详解九章算法》一书里出现了如图所示的表,即杨辉三角,这是数学史上的一个伟大成就在"杨辉三角"中,第 $n$ 行的所有数字之和为 $2^{n-1}$ ,若去除所有为 1 的项,依次构成数列 $2,3,3,4,6,4,5,10,10,5, \ldots$ ,则此数列的前 34 项和为
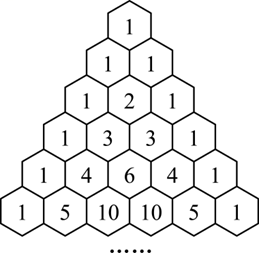
$\text{A.}$ 959
$\text{B.}$ 964
$\text{C.}$ 1003
$\text{D.}$ 1004
杨辉是我国古代数学史上一位著述丰富的数学家,著有《详解九章算法》《日用算法》和《杨辉算法》.杨辉三角的发现要比欧洲早500年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的.杨辉三角本身包含了很多有趣的性质,利用这些性质,可以解决很多数学问题,如开方、数列等
我们借助杨辉三角可以得到以下两个数列的和.
$$
\begin{aligned}
& 1+1+1+\cdots+1=n \\
& 1+2+3+\cdots+\mathrm{C}_{n-1}^1=\mathrm{C}_n^2
\end{aligned}
$$
若杨辉三角中第三斜行的数: $1,3,6,10,15, \ldots$ 构成数列 $\left\{a_n\right\}$ ,则关于数列 $\left\{a_n\right\}$ 叙述正确的是
$\text{A.}$ $a_n+a_{n+1}=(n+1)^2$
$\text{B.}$ $a_n+a_{n+1}=n^2$
$\text{C.}$ 数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $\mathrm{C}_n^3$
$\text{D.}$ 数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $\mathrm{C}_{n+1}^2$
多选题 (共 6 题 ),每题有多个选项正确
$\left(\sqrt{x}+\frac{1}{2 \sqrt[4]{x}}\right)^8$ 的展开式中系数最大的项是
$\text{A.}$ 第2项
$\text{B.}$ 第 3 项
$\text{C.}$ 第4项
$\text{D.}$ 第 5 项
若 $\left(2 x^2-\frac{1}{x}\right)^n$ 的展开式中有且仅有第五项的二项式系数最大,则展开式中系数最大的是
$\text{A.}$ 第二项
$\text{B.}$ 第三项
$\text{C.}$ 第四项
$\text{D.}$ 第五项
若 $f(x)=x^5-5 x^4+10 x^3-10 x^2+5 x-1$ ,则
$\text{A.}$ $f(x)$ 可以被 $(x-1)^3$ 整除
$\text{B.}$ $f(x+y+1)$ 可以被 $(x+y)^4$ 整除
$\text{C.}$ $f(30)$ 被 27 除的余数为 6
$\text{D.}$ $f(29)$ 的个位数为 6
$1.95^7$ 的计算结果精确到个位的近似值为
$\text{A.}$ 106
$\text{B.}$ 107
$\text{C.}$ 108
$\text{D.}$ 109
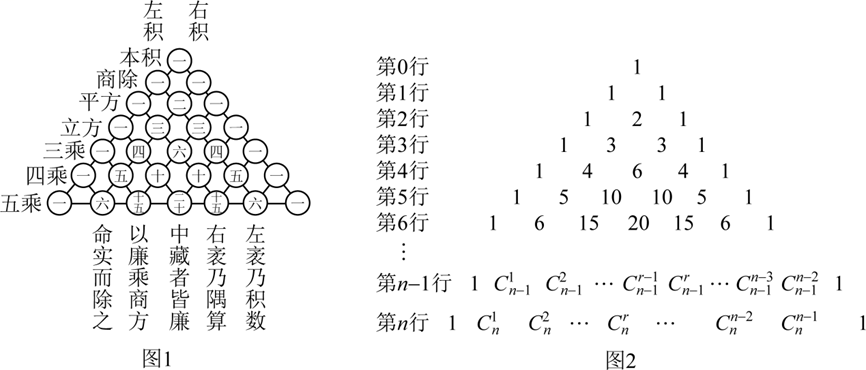
“杨辉三角”是二项式系数在三角形中的一种几何排列,在中国南宋数学家杨辉1261年所著的《详解九章算法》一书中就有出现.如图所示,在“杨辉三角”中,除每行两边的数都是1外,其余每个数都是其“肩上”的两个数之和,例如第4行的6为第3行中两个3的和.则下列命题中正确的是
$\text{A.}$ $\mathrm{C}_3^2+\mathrm{C}_4^2+\mathrm{C}_5^2+\cdots+\mathrm{C}_{10}^2=164$
$\text{B.}$ 在第 2022 行中第 1011 个数最大
$\text{C.}$ 记"杨辉三角"第 $n$ 行的第 $i$ 个数为 $a_i$ ,则 $\sum_{i=1}^{n+1}\left(2^{i-1} a_i\right)=3^n$
$\text{D.}$ 第 34 行中第 15 个数与第 16 个数之比为 $2: 3$
将杨辉三角中的每一个数 $\mathrm{C}_n^r$ 都换成 $\frac{1}{(n+1) \mathrm{C}_n^r}$ ,得到如图所示的分数三角形,称为莱布尼茨三角形.莱布尼茨三角形具有很多优美的性质,如从第 0 行开始每一个数均等于其"脚下"两个数之和,如果 $n \geq 2\left(n \in \mathrm{~N}^*\right)$ ,那么下面关于莱布尼茨三角形的结论正确的是
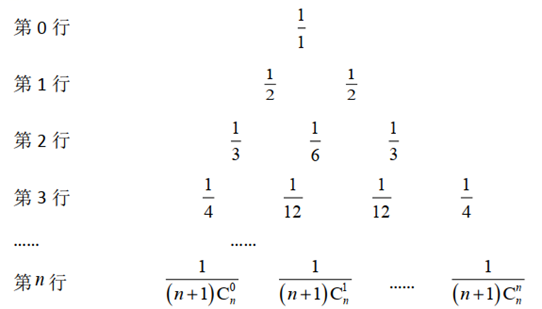
$\text{A.}$ 当 $n$ 是偶数时,中间的一项取得最大值,当 $n$ 是奇数时,中间的两项相等,且同时取得最大值
$\text{B.}$ $\frac{1}{(n+1) \mathrm{C}_n^1}=\frac{1}{(n+1) \mathrm{C}_n^0} \cdot \frac{1}{n \mathrm{C}_{n-1}^0}$
$\text{C.}$ $\frac{1}{(n+1) \mathrm{C}_n^r}=\frac{1}{(n+1) \mathrm{C}_n^{n-r}}(r \in \mathrm{~N}, 0 \leq r \leq n)$
$\text{D.}$ $\frac{1}{(n+1) \mathrm{C}_n^{r-1}}+\frac{1}{(n+1) \mathrm{C}_n^r}=\frac{1}{n \mathrm{C}_n^{r-1}}(r \in \mathrm{~N}, 1 \leq r \leq n)$
填空题 (共 5 题 ),请把答案直接填写在答题纸上
$\left(1-\frac{y}{x}\right)(x+y)^8$ 的展开式中 $x^2 y^6$ 的系数为 $\_\_\_\_$ (用数字作答)
已知 $(a+x)(1+x)^6$ 的展开式中 $x^2$ 的系数为 21 ,则 $a=$
在 $(\sqrt{x}-1)^6(2 \sqrt[3]{x}+1)^9$ 的展开式中,$x$ 的系数为
求 $1.02^5$ 的近似值.(精确到两位小数)
已知等差数列 $\left\{a_n\right\}$ ,对任意 $n \in N^{+}$都有 $a_1 \mathrm{C}_n^0+a_2 \mathrm{C}_n^1+a_3 \mathrm{C}_n^2+\mathrm{...}+a_{n+1} \mathrm{C}_n^n=n \cdot 2^{n+1}$成立,则数列 $\left\{\frac{1}{a_{n+1} a_{n+2}}\right\}$ 的前 $n$ 项和 $T_n=$
解答题 (共 1 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
$(x+1)^6\left(x^2+2 x+1\right)$ 展开式中 $x^3$ 的系数为