将杨辉三角中的每一个数 $\mathrm{C}_n^r$ 都换成 $\frac{1}{(n+1) \mathrm{C}_n^r}$ ,得到如图所示的分数三角形,称为莱布尼茨三角形.莱布尼茨三角形具有很多优美的性质,如从第 0 行开始每一个数均等于其"脚下"两个数之和,如果 $n \geq 2\left(n \in \mathrm{~N}^*\right)$ ,那么下面关于莱布尼茨三角形的结论正确的是
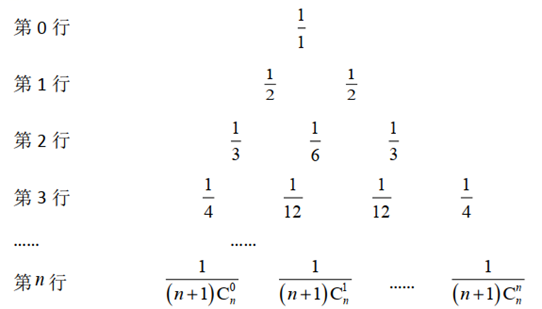
A
当 $n$ 是偶数时,中间的一项取得最大值,当 $n$ 是奇数时,中间的两项相等,且同时取得最大值
B
$\frac{1}{(n+1) \mathrm{C}_n^1}=\frac{1}{(n+1) \mathrm{C}_n^0} \cdot \frac{1}{n \mathrm{C}_{n-1}^0}$
C
$\frac{1}{(n+1) \mathrm{C}_n^r}=\frac{1}{(n+1) \mathrm{C}_n^{n-r}}(r \in \mathrm{~N}, 0 \leq r \leq n)$
D
$\frac{1}{(n+1) \mathrm{C}_n^{r-1}}+\frac{1}{(n+1) \mathrm{C}_n^r}=\frac{1}{n \mathrm{C}_n^{r-1}}(r \in \mathrm{~N}, 1 \leq r \leq n)$
E
F