杨辉是我国古代数学史上一位著述丰富的数学家,著有《详解九章算法》《日用算法》和《杨辉算法》.杨辉三角的发现要比欧洲早500年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的.杨辉三角本身包含了很多有趣的性质,利用这些性质,可以解决很多数学问题,如开方、数列等
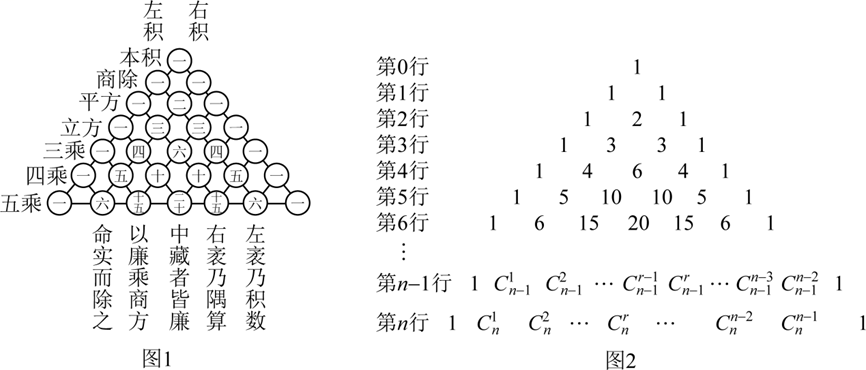
我们借助杨辉三角可以得到以下两个数列的和.
$$
\begin{aligned}
& 1+1+1+\cdots+1=n \\
& 1+2+3+\cdots+\mathrm{C}_{n-1}^1=\mathrm{C}_n^2
\end{aligned}
$$
若杨辉三角中第三斜行的数: $1,3,6,10,15, \ldots$ 构成数列 $\left\{a_n\right\}$ ,则关于数列 $\left\{a_n\right\}$ 叙述正确的是
A
$a_n+a_{n+1}=(n+1)^2$
B
$a_n+a_{n+1}=n^2$
C
数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $\mathrm{C}_n^3$
D
数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $\mathrm{C}_{n+1}^2$
E
F