某地区的疾控机构为了考察药物A对某疾病的预防效果,在该地区随机抽取96人,调查得到的统计数据如下表所示


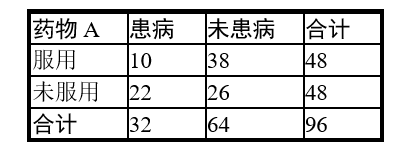
（1）依据 $\alpha=0.01$ 的独立性检验，能否认为药物 A 对预防该疾病有效果？
（2）已知治愈一位服用药物 A 的该疾病患者需要 2 个疗程，治愈一位未服用药物 A 的该疾病患者需要 3 个疗程．从该地区随机抽取 1 人，调查其是否服用药物 A、是否患该疾病．若未患病，则无需治疗；若患病，则对其进行治疗并治愈．求所需疗程数的数学期望．

$$
\text { 附: } \chi^2=\frac{n(a d-b c)^2}{(a+b)(c+d)(a+c)(b+d)} \text {, 其中 } n=a+b+c+d \text {. }
$$

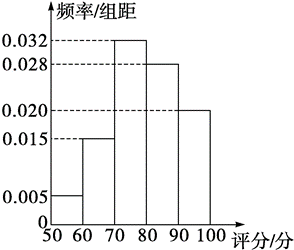
某高中采用多维评分的方式进行综合素质评价．下图是该校高三学生＂运动与健康＂评价结果的频率分布直方图，评分在区间［90，100），［70，90），［60，70），［50，60）内，分别对应为 A，B，C，D四个等级。为了进一步引导学生对运动与健康的重视，初评获 A 等级的学生不参加复评，等级不变，对其余学生学校将进行一次复评。复评中，原获 B 等级的学生有 $\frac{1}{4}$ 的概率提升为 A 等级；原获 C 等级的学生有 $\frac{1}{5}$ 的概率提升为 B 等级；原获 D 等级的学生有 $\frac{1}{6}$ 的概率提升为 C 等级。用频率估计概率，每名学生复评结果相互独立。
（1）若初评中甲获得 B 等级，乙、丙获得 C 等级，记甲、乙、丙三人复评后等级为 B 等级的人数为 $\xi$ ，求 $\xi$ 的分布列和数学期望；
（2）从全体高三学生中任选 1 人，在已知该学生是复评晋级的条件下，求他初评是 C 等级的概率．

2023年春季以来,各地出台了促进经济发展的各种措施,经济增长呈现稳中有进的可喜现象.服务业的消费越来越火爆,一些超市也纷纷加大了广告促销.现随机抽取7家超市,得到其广告支出x(单位:万元)与销售额y(单位:万元)的数据如下.


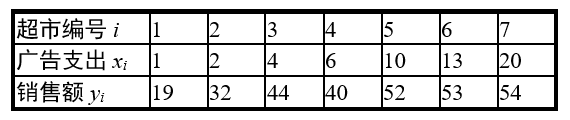
（1）已知 $x$ 和 $y$ 具有线性相关关系，建立 $y$ 关于 $x$ 的经验回归方程；（系数精确到 0.01 ）
（2）若将超市的销售额 $y$ 与广告支出 $x$ 的比值称为该超市的广告效率值 $\mu$ ，当 $\mu \geqslant 10$ 时，称该超市的广告为＂好广告＂。从这 7 家超市中随机抽取 4 家超市，记这 4 家超市中＂好广告＂的超市数为 $X$ ，求 $X$ 的分布列与期望．
附：$\sum_{i=1}^7 x_i y_i=2788, \sum_{i=1}^7 x_i^2=726, \sum_{i=1}^7 y_i^2=13350$ ，经验回归直线 $\hat{y}=\hat{a}+\hat{b} x$ 中斜率和截距的最小二乘估计分别为 $\hat{b}=\frac{\sum_{i=1}^n x_i y_i-n \bar{x} \bar{y}}{\sum_{i=1}^n x_i^2-n \bar{x}^2}, \hat{a}=\bar{y}-\hat{b} \bar{x}$ ．

4．为了引导青少年抵制不良游戏，适度参与益脑游戏，某游戏公司开发了一款益脑游戏，在内测时收集了玩家每一关的平均过关时间，如下表：


计算得到一些统计量的值为 $\sum_{i=1}^6 u_i=28.5, \sum_{i=1}^6 x_i u_i=106.05$ ，其中，$u=\ln y$ ．
（1）若用模型 $y=a \mathrm{e}^{b x}$ 拟合 $y$ 与 $x$ 的关系，根据提供的数据，求出 $y$ 与 $x$ 的经验回归方程．
（2）制定游戏规则如下：玩家在每关的平均过关时间内通过可获得积分 2 分并进入下一关，否则获得 -1分且该轮游戏结束．甲通过练习，前 3 关都能在平均时间内过关，后面 3 关能在平均时间内通过的概率均为 $\frac{4}{5}$ ，若甲玩一轮此款益脑游戏，求＂甲获得的积分 $X$＂的分布列和数学期望。
参考公式：对于一组数据 $\left(x_i, y_i\right)(i=1,2,3, \cdots, n)$ ，其经验回归直线 $\hat{y}=\hat{b} x+\hat{a}$ 的斜率和截距的最小二乘估计分别为 $\hat{b}=\frac{\sum_{i=1}^n x_i y_i-n \bar{x} \bar{y}}{\sum_{i=1}^n x_i^2-n \bar{x}^2}, \hat{a}=\bar{y}-\hat{b} \bar{x}$ ．

某商场为了回馈广大顾客，设计了一个抽奖活动，在抽奖箱中放 10 个除颜色外完全相同的小球，其中 5 个为红色， 5 个为白色。抽奖方式为：每名顾客进行两次抽奖，每次抽奖从抽奖箱中一次性摸出两个小球。如果每次抽奖摸出的两个小球颜色相同即为中奖，两个小球颜色不同即为不中奖。
（1）若规定第一次抽奖后将球放回抽奖箱，再进行第二次抽奖，求中奖次数 $X$ 的分布列和数学期望；
（2）若规定第一次抽奖后不将球放回抽奖箱，直接进行第二次抽奖，求中奖次数 $Y$ 的分布列和数学期望。

某技术部门对工程师进行达标等级考核，需要进行两轮测试，每轮测试的成绩在 90 分及以上的定为该轮测试通过，只有通过第一轮测试的人员才能进行第二轮测试，两轮测试的过程相互独立，并规定：
① 两轮测试均通过的定为一级工程师；
② 仅通过第一轮测试，而第二轮测试没通过的定为二级工程师；
③ 第一轮测试没通过的不予定级．
现有某公司的甲、乙、丙三位工程师参加等级考核，已知他们通过第一轮测试的概率分别为 $\frac{1}{3}, \frac{2}{3}, \frac{2}{3}$ ，通过第二轮测试的概率均为 $\frac{1}{2}$ ．
（1）求经过本次考核，甲、乙、丙三位工程师中恰有两位被定为一级工程师的概率．
（2）公司为鼓励工程师参加等级考核设置两套奖励方案。
方案一：定为一级工程师的奖励 2000 元，定为二级工程师的奖励 1500 元，未定级的给予鼓励奖 500元。
方案二：定为一级或二级工程师的均奖励 2000 元，未定级的不予奖励。
采用哪套方案，公司的奖励支出会更少？