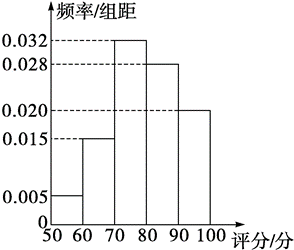
某高中采用多维评分的方式进行综合素质评价．下图是该校高三学生＂运动与健康＂评价结果的频率分布直方图，评分在区间［90，100），［70，90），［60，70），［50，60）内，分别对应为 A，B，C，D四个等级。为了进一步引导学生对运动与健康的重视，初评获 A 等级的学生不参加复评，等级不变，对其余学生学校将进行一次复评。复评中，原获 B 等级的学生有 $\frac{1}{4}$ 的概率提升为 A 等级；原获 C 等级的学生有 $\frac{1}{5}$ 的概率提升为 B 等级；原获 D 等级的学生有 $\frac{1}{6}$ 的概率提升为 C 等级。用频率估计概率，每名学生复评结果相互独立。
（1）若初评中甲获得 B 等级，乙、丙获得 C 等级，记甲、乙、丙三人复评后等级为 B 等级的人数为 $\xi$ ，求 $\xi$ 的分布列和数学期望；
（2）从全体高三学生中任选 1 人，在已知该学生是复评晋级的条件下，求他初评是 C 等级的概率．