浙江省湖州市2022-2023学年七年级上学期中数学试题

导出试卷

浙江省湖州市2022-2023学年七年级上学期中数学试题

一、单选题（共 10 题），每题只有一个选项正确

5

的相反数是

A.

- \frac{1}{5}

B.

\frac{1}{5}

C.

- 5

D.

5

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

2. 体现我国先进核电技术的“华龙一号”, 年发电能力相当于减少二氧化碳排放 16320000 吨,数 16320000 用科学记数法表示为

A.

1632 \times 10^{4}

B.

1.632 \times 10^{7}

C.

1.632 \times 10^{6}

D.

16.32 \times 10^{5}

查看分享下载此题点赞(0) 收藏(1) 错题本(1) 白板加入试卷

3. 若气温零上

2^{\circ} C

记作

+ 2^{\circ} C

, 则气温零下

3^{\circ} C

记作

A.

- 3^{\circ} C

B.

- 1^{\circ} C

C.

+ 1^{\circ} C

D.

+ 5^{\circ} C

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

4. 当

x = 2

时, 代数式

3 x - 1

的值是

A.

- 5

B.

1

C.

4

D.

5

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

5. 与

- 3 \frac{1}{2}

相等的是

A.

- 3 - \frac{1}{2}

B.

3 - \frac{1}{2}

C.

- 3 + \frac{1}{2}

D.

3 + \frac{1}{2}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

6. 由四舍五人法得到的近似数

42.3

万精确到的数位是

A.

十分位

B.

十位

C.

百位

D.

千位

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

7. 下列说法正确的是

A.

25 的平方根是 5

B.

3 是 9 的一个平方根

C.

负数没有立方根

D.

立方根等于它本身的数是 0,1

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

8. 已知

44^{2} = 1936, 45^{2} = 2025, 46^{2} = 2116, 47^{2} = 2209

. 若

n

为整数且

n < \sqrt{2022} < n + 1

, 则

n

值为

A.

B.

C.

D.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

9. 如图 1 , 点

A, B, C

是数轴上从左到右排列的三个点, 分别对应的数为

- 5, b, 4

, 某同学将刻度尺如图 2 放置, 使刻度尺上的数字 0 对齐数轴上的点

A

, 发现点

B

对应刻度

1.8

cm

, 点

C

对齐刻度

5.4 cm

则数轴上点

B

所对应的数

b

为

A.

3

B.

- 1

C.

- 2

D.

- 3

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

10. 如图所示, 第一个图形共 6 个小圆圈,第二个图形共 12 个小圆圈,第三个图形共 20 个小圆圈, 则按此规律 (每个图形依次多一条边), 第 8 个图形共 ( ) 个小圆圈.

A.

B.

C.

D.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

二、填空题（共 6 题），请把答案直接填写在答题纸上

11. 化简

- (- 3.6)

的结果是

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

12. 把式子

(- 2) \times (- 2) \times (- 2) \times (- 2)

写成乘方的形式

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

13.

x

的 3 倍与

y

的差是

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

14. 一个数与

(- \frac{3}{4})

的积为

\frac{2}{3}

, 则这个数是

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

15. 有一个数值转换器, 流程如下:

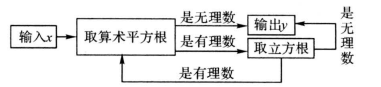
当输人的

x

值为 64 时, 输出的

y

值是

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

16. 根据图示的对话, 式子

5 a + 5 b - c + 2 d

的值是

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

三、解答题（共 10 题），解答过程应写出必要的文字说明、证明过程或演算步骤

17. 把下列各数的序号分别填人相应的横线上.
①

- 5

②

- 3.14

③

\sqrt{4}

④

- \frac{π}{3}

⑤

0.1010010001 \dots

(每两个 1 之间依次多一个 0 )

(1) 整数:
(2)分数:
(3) 无理数:

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

18. 计算:
(1)

3 - 4 + 2

;
(2)

- 2.5 \div \frac{5}{16} \times (- \frac{1}{8})

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

19. 计算:
(1)

(- \frac{1}{12} - \frac{1}{36} + \frac{1}{6}) \times (- 36)

;
(2)

\sqrt[3]{- 27} - 4 \div (- 2)

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

20. 小双在计算:

- (- 1)^{2022} - (- 2)^{3} \div (- 8)

时, 步骤如下:

解: 原式 =

\begin{aligned} = 2022 - (- 8) \div (- 8) \dots ① \\ = 2022 - 1 \dots ② \\ = 2021 \dots ③ \end{aligned}

(1)小双的计算过程中开始出现错误的步骤是 ; (填序号)
(2) 请给出正确的解题过程.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

21. 生命在于运动, 小双每天坚持练习跳绳. 某一天, 小双以 1 分钟跳 160 个为目标, 并把 10 次 1 分钟跳的数量记录如下 (超过 160 个的部分记为 “+”, 少于 160 个的部分记为 “-”) :

- 9, - 10, - 2, + 12, + 10, - 11, + 13, - 2, + 6, + 7

.
(1) 小双在这 10 次跳绳练习中, 1 分钟最少跳了多少个?
(2) 小双在这 10 次跳绳练习中累计跳绳多少个?

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

22. 七年级小减同学在学习完第二章《有理数》后, 对运算产生了浓厚的兴趣. 她借助有理数的运算, 定义了一种新运算“

\oplus

”, 规则如下:

a \oplus b = a \times b + 2 \times a

.
(1)求

(- 2) \oplus (- 3)

的值;
(2)求

(- 5) \oplus [2 \oplus (- 4)]

的值.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

23. 某服装厂生产一种围巾和手套, 每条围巾的定价为 50 元, 每双手套的定价为 20 元. 厂方在开展促销活动期间, 向客户提供两种优惠方案:
方案(1) : 买一条围巾送一双手套;
方案(2): 围巾和手套都按定价的

80 %

付款.
现某客户要到该服装厂购买围巾 20 条, 手套

x

双

(x > 20)

(1) 若该客户按方案(1)购买, 则需付款（　　）元 (用含

x

的代数式表示); 若该客户按方案(2)购买, 则需付款（　　）元 (用含

x

的代数式表示);
(2)若

x = 30

, 则通过计算说明此时按哪种方案购买较为合算.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

24. 如图甲, 这是由 8 个同样大小的立方体组成的魔方, 总体积为

V {cm}^{3}

.
(1)求这个魔方的棱长; (用代数式表示)
(2) 当魔方体积

V = 64 {cm}^{3}

时,
(1)图甲中阴影部分是一个正方形

A B C D

, 求出阴影部分的面积;
(2)把正方形

A B C D

放置在数轴上, 如图乙所示, 使得点

A

与数 1 重合, 则

D

在数轴上表示的数为
(3) 在图丙的

5 \times 5

方格中, 画一个面积为 13 的格点正方形 (四个顶点都在方格的顶点上); 并把图中的数轴补充完整, 然后用圆规在数轴上表示实数

\sqrt{13}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

25. 如图甲, 这是由 8 个同样大小的立方体组成的魔方, 总体积为

V {cm}^{3}

.
(1)求这个魔方的棱长; (用代数式表示)
(2) 当魔方体积

V = 64 {cm}^{3}

时,
(1)图甲中阴影部分是一个正方形

A B C D

, 求出阴影部分的面积;
(2)把正方形

A B C D

放置在数轴上, 如图乙所示, 使得点

A

与数 1 重合, 则

D

在数轴上表示的数为
(3) 在图丙的

5 \times 5

方格中, 画一个面积为 13 的格点正方形 (四个顶点都在方格的顶点上); 并把图中的数轴补充完整, 然后用圆规在数轴上表示实数

\sqrt{13}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

26. 生命在于运动, 小双每天坚持练习跳绳. 某一天, 小双以 1 分钟跳 160 个为目标, 并把 10 次 1 分钟跳的数量记录如下 (超过 160 个的部分记为 “ ”, 少于 160 个的部分记为 “-”) :

- 9, - 10, - 2, 12, 10, - 11, 13, - 2, 6, 7

.
(1) 小双在这 10 次跳绳练习中, 1 分钟最少跳了多少个?
(2) 小双在这 10 次跳绳练习中累计跳绳多少个?

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

非会员每天可以查看15道试题。开通会员，海量试题无限制查看。

无限看试题
下载试题
组卷

开通会员

热点推荐

试卷二维码

分享此二维码到群，让更多朋友参与

试卷白板

试卷白板提供了一个简单的触摸书写板，可供老师上课、或者视频直播时，直接利用白板给学生讲解试题，如有意见，欢迎反馈。