单选题 (共 4 题 ),每题只有一个选项正确
已知向量 $\vec{a}=(2,1), \vec{b}=(-2,4)$ ,则 $|\vec{a}-\vec{b}|$
$\text{A.}$ 2
$\text{B.}$ 3
$\text{C.}$ 4
$\text{D.}$ 5
已知向量 $\vec{a}=(2,3), \vec{b}=(3,2)$ ,则 $|\vec{a}-\vec{b}|=$
$\text{A.}$ $\sqrt{2}$
$\text{B.}$ 2
$\text{C.}$ $5 \sqrt{2}$
$\text{D.}$ 50
在 $\triangle A B C$ 中,$A D$ 为 $B C$ 边上的中线,$E$ 为 $A D$ 的中点,则 $\overrightarrow{E B}=$
$\text{A.}$ $\frac{3}{4} \overrightarrow{A B}-\frac{1}{4} \overrightarrow{A C}$
$\text{B.}$ $\frac{1}{4} \overrightarrow{A B}-\frac{3}{4} \overrightarrow{A C}$
$\text{C.}$ $\frac{3}{4} \overrightarrow{A B}+\frac{1}{4} \overrightarrow{A C}$
$\text{D.}$ $\frac{1}{4} \overrightarrow{A B}+\frac{3}{4} \overrightarrow{A C}$
在 $\triangle A B C$ 中,$B E$ 是边 $A C$ 上的中线,$O$ 是 $B E$ 的中点,若 $\overrightarrow{A B}=\boldsymbol{a}, \overrightarrow{A C}=\boldsymbol{b}$ ,则 $\overrightarrow{A O}$ 等于()
$\text{A.}$ $\frac{1}{2} \boldsymbol{a}+\frac{1}{2} \boldsymbol{b}$
$\text{B.}$ $\frac{1}{2} a+\frac{1}{3} b$
$\text{C.}$ $\frac{1}{4} \boldsymbol{a}+\frac{1}{2} \boldsymbol{b}$
$\text{D.}$ $\frac{1}{2} \boldsymbol{a}+\frac{1}{4} \boldsymbol{b}$
多选题 (共 1 题 ),每题有多个选项正确
下列说法不正确的是( )
$\text{A.}$ 若 $\vec{a}=(1,2), \vec{b}=(1,-1)$ ,且 $\vec{a}$ 与 $\vec{a}+\lambda \vec{b}$ 的夹角为锐角,则 $\lambda$ 的取值范围是 $(-\infty, 5)$
$\text{B.}$ 若 $A, B, C$ 不共线,且 $\overrightarrow{O P}=2 \overrightarrow{O A}-4 \overrightarrow{O B}+3 \overrightarrow{O C}$ ,则 $P, A, B 、 C$ 四点共面
$\text{C.}$ 对同一平面内给定的三个向量 $\vec{a}, \vec{b}, \vec{c}$ ,一定存在唯一的一对实数 $\lambda, \mu$ ,使得 $\vec{a}=\lambda \vec{b}+\mu \vec{c}$ .
$\text{D.}$ $\triangle A B C$ 中,若 $\overrightarrow{A B} \cdot \overrightarrow{B C} < 0$ ,则 $\triangle A B C$ 一定是钝角三角形.
填空题 (共 9 题 ),请把答案直接填写在答题纸上
已知向量 $\vec{a}=(2,5), \vec{b}=(\lambda, 4)$ ,若 $\vec{a} / / \vec{b}$ ,则 $\lambda=$ $\qquad$ .
已知向量 $\boldsymbol{a}=(m, 2), \boldsymbol{b}=(3,-6)$ ,若 $\boldsymbol{a}=\lambda \boldsymbol{b}$ ,则实数 $m$ 的值是( )
A.-4
B.-1
C. 1
D. 4
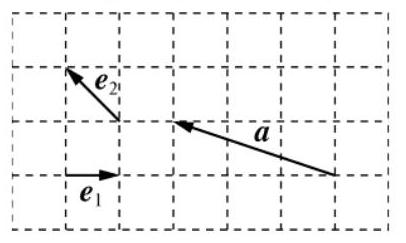
如图,向量 $\boldsymbol{e}_{1}, \boldsymbol{e}_{2}, \boldsymbol{a}$ 的起点与终点均在正方形网格的格点上,则向量 $\boldsymbol{a}$ 可用基底 $\boldsymbol{e}_{1}, \boldsymbol{e}_{2}$ 表示为 $\qquad$ .
已知点 $M$ 是 $\triangle A B C$ 的边 $B C$ 的中点,点 $E$ 在边 $A C$ 上,且 $\overrightarrow{E C}=2 \overrightarrow{A E}$ ,则向量 $\overrightarrow{E M}=$ $\qquad$ (用 $\overrightarrow{A B}, \overrightarrow{A C}$ 表示)。
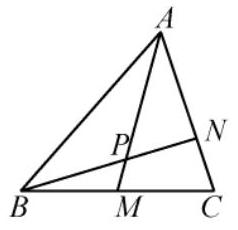
如图,在 $\triangle A B C$ 中,$M$ 是 $B C$ 的中点,点 $N$ 在 $A C$ 上,且 $A N=2 N C, A M$ 与 $B N$ 相交于点 $P$ ,求 $A P: P M$与 $B P: P N$ 的值.
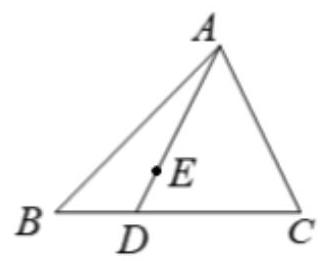
如图,在 $\triangle A B C$ 中, $\overrightarrow{B D}=\frac{1}{3} \overrightarrow{B C}$ ,点 $E$ 在线段 $A D$ 上移动(不含端点),若 $\overrightarrow{A E}=\lambda \overrightarrow{A B}+\mu \overrightarrow{A C}$ ,则 $\frac{\lambda}{\mu}=$ $\qquad$ , $\lambda^{2}-\mu$ 的最小值为 $\qquad$ .
已知点 $A(2,1), B(3,5), C(3,2), \overrightarrow{A P}=\overrightarrow{A B}+t \overrightarrow{A C}(t \in \mathbf{R})$ ,若点 $P$ 在第二象限,则实数 $t$ 的取值范围是 $\qquad$ .
已知向量 $\vec{a}=(m+4, m), \vec{b}=(3,1)$ ,且 $\vec{a} / / \vec{b}$ ,则 $m=$ $\qquad$ .
在平行四边形 $A B C D$ 中,$E$ 是线段 $B D$ 的中点,若 $\overrightarrow{A B}=m \overrightarrow{A D}+n \overrightarrow{E C}$ ,则 $m-n=$ $\qquad$ .
解答题 (共 4 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
在平面直角坐标系 $x O y$ 中,已知点 $A(1,1), B(2,3), C(3,2)$ .
(1)若 $\overrightarrow{P A}+\overrightarrow{P B}+\overrightarrow{P C}=0$ ,求 $\overrightarrow{O P}$ 的坐标;
(2)若 $\overrightarrow{O P}=m \overrightarrow{A B}+n \overrightarrow{A C}(m, n \in \mathbf{R})$ ,且点 $P$ 在函数 $y=x+1$ 的图象上,求 $m-n$ 的值.
、已知 $A(-2,4), B(3,-1), C(-3,-4)$ .设 $\overrightarrow{A B}=\boldsymbol{a}, \overrightarrow{B C}=\boldsymbol{b}, \overrightarrow{C A}=\boldsymbol{c}$ ,且 $\overrightarrow{C M}=3 \boldsymbol{c}, \overrightarrow{C N}=-2 \boldsymbol{b}$ ,
(1)求 $3 \boldsymbol{a}+\boldsymbol{b}-3 \boldsymbol{c}$ ;
(2)求满足 $\boldsymbol{a}=m \boldsymbol{b}+n \boldsymbol{c}$ 的实数 $m, n$ ;
(3)求 $M, N$ 的坐标及向量 $\overrightarrow{M N}$ 的坐标.
平面内给定三个向量 $\boldsymbol{a}=(3,2), \boldsymbol{b}=(-1,2), \boldsymbol{c}=(4,1)$ .
(1)若 $(\boldsymbol{a}+k \boldsymbol{c}) / /(2 \boldsymbol{b}-\boldsymbol{a})$ ,求实数 $k$ ;
(2)若 $\boldsymbol{d}$ 满足 $(\boldsymbol{d}-\boldsymbol{c}) / /(\boldsymbol{a}+\boldsymbol{b})$ ,且 $|\boldsymbol{d}-\boldsymbol{c}|=\sqrt{5}$ ,求 $\boldsymbol{d}$ 的坐标.
已知 $O$ 为坐标原点,向量 $\overrightarrow{O A}=(3,-4), \overrightarrow{O B}=(5,-3), \overrightarrow{O C}=(4-m, m+2)$ .若点 $D\left(0, \frac{3}{2} m\right)$ ,求证:对任意实数 $m$ ,都有 $\overrightarrow{A B} / / \overrightarrow{D C}$ .