单选题 （共 10 题 ），每题只有一个选项正确
函数 $y=\left(3^x-3^{-x}\right) \cos x$ 在区间 $\left[-\frac{\pi}{2}, \frac{\pi}{2}\right] $ 的图象大致为
$\text{A.}$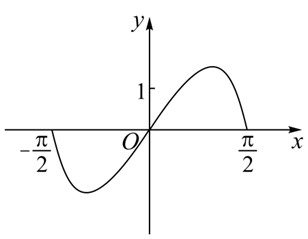 
$\text{B.}$ 
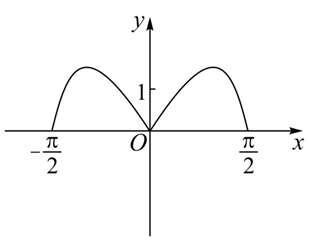$\text{C.}$ 
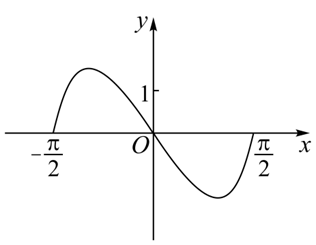$\text{D.}$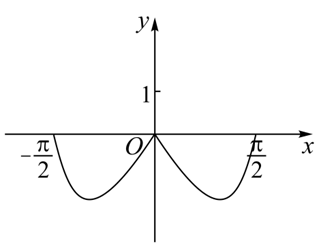 
如图是下列四个函数中的某个函数在区间 $[-3,3]$ 的大致图象，则该函数是
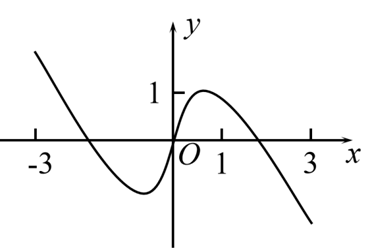
$\text{A.}$ $y=\frac{-x^3+3 x}{x^2+1}$
$\text{B.}$ $y=\frac{x^3-x}{x^2+1}$
$\text{C.}$ $y=\frac{2 x \cos x}{x^2+1}$
$\text{D.}$ $y=\frac{2 \sin x}{x^2+1}$
设函数 $f(x)$ 的定义域为 R ，满足 $f(x+1)=2 f(x)$ ，且当 $x \in(0,1]$ 时，$f(x)=x(x-1)$ ．若对任意 $x \in(-\infty, m]$ ，都有 $f(x) \geq-\frac{8}{9}$ ，则 $m$ 的取值范围是
$\text{A.}$ $\left(-\infty, \frac{9}{4}\right]$
$\text{B.}$ $\left(-\infty, \frac{7}{3}\right]$
$\text{C.}$ $\left(-\infty, \frac{5}{2}\right]$
$\text{D.}$ $\left(-\infty, \frac{8}{3}\right]$
如图，函数 $f(x)$ 的图象是曲线 $O A B$ ，其中点 $O, A, B$ 的坐标分别为 $(0,0),(1,2),(3$ ， 1），则 $f\left(\frac{1}{f(3)}\right)$ 的值为
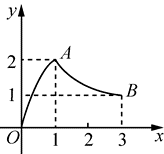
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ $\frac{7}{4}$
$\text{D.}$ $\frac{5}{4}$
设函数 $f(x)=\left\{\begin{array}{ll}2^{-} x, & x \leqslant 0, \\ 1, & x>0,\end{array}\right.$ 则满足 $f(x+1) < f(2 x)$ 的 $x$ 的取值范围是 $($
$\text{A.}$ $(-\infty, 1)$
$\text{B.}$ $(0,+\infty)$
$\text{C.}$ $(-1,0)$
$\text{D.}$ $(-\infty, 0)$
函数 $f(x)=\frac{1-x^2}{e^x}$ 的图象大致为
$\text{A.}$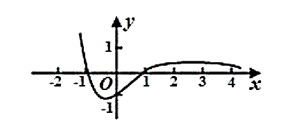 
$\text{B.}$ 
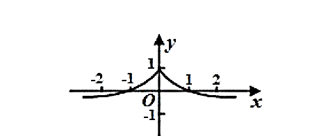$\text{C.}$ 
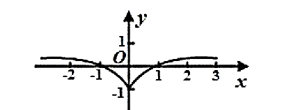$\text{D.}$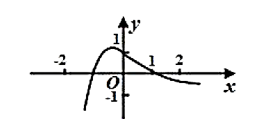 
函数 $y=\frac{\ln |x|}{x^2+2}$ 的图象大致为
$\text{A.}$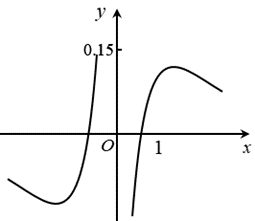 
$\text{B.}$ 
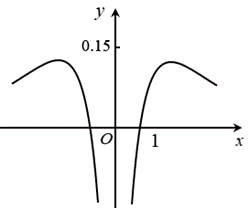$\text{C.}$ 
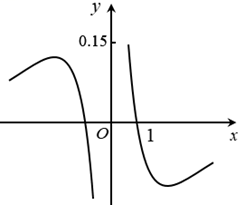$\text{D.}$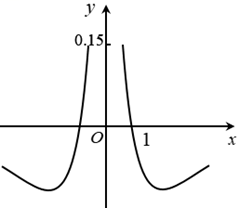 
已知 $\left(\frac{1}{3}\right)^a=\log _3 a, 3^b=\log _{\frac{1}{3}} b,\left(\frac{1}{3}\right)^c=\log _{\frac{1}{3}} c$ ，则 $a, b, c$ 的大小关系是
$\text{A.}$ $c < b < a$
$\text{B.}$ $a < b < c$
$\text{C.}$ $b < c < a$
$\text{D.}$ $b < a < c$
已知函数 $f(x)=\left\{\begin{array}{l}\frac{x}{x-1}, x \leq 0, \\ \frac{\ln x}{x}, x>0 .\end{array}\right.$ 若关于 $x$ 的方程，$f(x)=x+a$ 无实根，则实数 $a$ 的取值范围为（ ）
$\text{A.}$ $(-\infty, 0) U \left(\frac{1}{ e }, 1\right)$
$\text{B.}$ $(-1,0)$
$\text{C.}$ $\left(0, \frac{1}{e}\right)$
$\text{D.}$ $(0,1)$
我国著名数学家华罗庚曾说：＂数缺形时少直观，形少数时难入微，数形结合白般好，隔离分家万事休．＂在数学的学习和研究中，有时可凭借函数的图象分析函数解析式的特征．已知函数 $f(x)$ 的部分图象如图所示，则函数 $f(x)$ 的解析式可能为
$\text{A.}$ $f(x)=\frac{2 x}{1-|x|}$
$\text{B.}$ $f(x)=\frac{2 x}{x^2+1}$
$\text{C.}$ $f(x)=\frac{2 x}{x^2-1}$
$\text{D.}$ $f(x)=\frac{x^2+1}{x^2-1}$
多选题 （共 4 题 ），每题有多个选项正确
关于函数 $f(x)=|\ln | 2-x| |$ ，下列说法中正确的有（ ）
$\text{A.}$ $f(x)$ 在区间 $(1,2)$ 上单调递增
$\text{B.}$ $f(x)$ 的图象关于直线 $x=2$ 对称
$\text{C.}$ 若 $x_1 \neq x_2, f\left(x_1\right)=f\left(x_2\right)$ ，则 $x_1+x_2=4$
$\text{D.}$ $f(x)$ 有且仅有两个零点
函数 $f(x)=\frac{x}{x^2+a}$ 的图象可能是
$\text{A.}$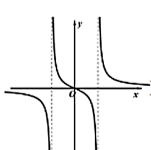 
$\text{B.}$ 
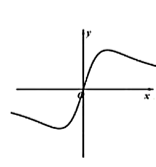$\text{C.}$ 
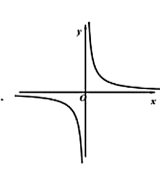$\text{D.}$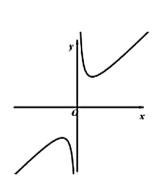 
已知函数 $f(x)=x|x-a|, ~ a \in R$ ，下列判断中，正确的有（ ）
$\text{A.}$ 存在 $k \in R$ ，函数 $y=f(x)-k$ 有 4 个零点
$\text{B.}$ 存在常数 $a$ ，使 $f(x)$ 为奇函数
$\text{C.}$ 若 $f(x)$ 在区间 $[0,1]$ 上最大值为 $f(1)$ ，则 $a$ 的取值范围为 $a \leq 2 \sqrt{2}-2$ 或 $a \geq 2$
$\text{D.}$ 存在常数 $a$ ，使 $f(x)$ 在 $[1,3]$ 上单调递减
已知 $f(x)$ 是定义在 $R$ 上的偶函数，且 $f(x+3)=f(x-1)$ ，若当 $x \in[0,2]$ 时，$f(x)=2^x-1$ ，则下列结论正确的是
$\text{A.}$ 当 $x \in[-2,0]$ 时，$f(x)=2^{-x}-1$
$\text{B.}$ $f(2019)=1$
$\text{C.}$ $y=f(x)$ 的图象关于点 $(2,0)$ 对称
$\text{D.}$ 函数 $g(x)=f(x)-\log _2 x$ 有 3 个零点
填空题 （共 1 题 ），请把答案直接填写在答题纸上
已知定义在 $R$ 上的函数 $f(x)$ 满足：（1）$f(x)+f(2-x)=0$ ；（2）$f(x)-f(-2-x)=0$ ；（3）在区间 $[-1$ ， 1］上的表达式为 $f(x)=\left\{\begin{array}{ll}\sqrt{1-x^2}, & -1 \leqslant x \leqslant 0, \\ 1-x, & 0 < x \leqslant 1,\end{array}\right.$ 则函数 $f(x)$ 与 $g(x)=\left\{\begin{array}{ll}2^x, & x \leqslant 0, \\ \log _{\frac{1}{2}} x, & x>0\end{array}\right.$ 的图象在区间 $[-3,3]$ 上的交点的个数为