一、单选题 （共 5 题，每小题 2 分，共 10 分）
已知一射手在唡次独立射击中至少命中目标一次的概率为 0.96 , 则该射手每次射击的命中率为
$\text{A.}$ 0.04
$\text{B.}$ 0.2
$\text{C.}$ 0.8
$\text{D.}$ 0.96
设随机变量 $X$ 啒从犙数为 $\lambda$ 的泊松分布, 且满足 $P\{\dot{X}=1\}=\frac{2}{3} P\{X=3\}$, 则 $\lambda=$
$\text{A.}$ 1
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
设二维随机变量 $(X, Y)$ 的分布律
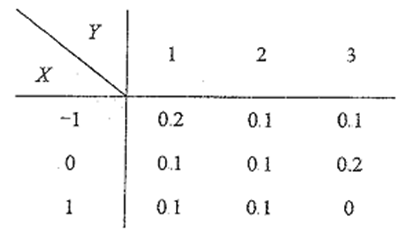
则 $P\{X+Y \leq 1\}=$
$\text{A.}$ 0.4
$\text{B.}$ 0.3
$\text{C.}$ 0.2
$\text{D.}$ 0.1
设 $x_1, x_2, \cdots, x_n$ 是来自正态总体 $N\left(\mu, \sigma^2\right)$ 的样本, $\bar{x}, s^2$ 分别为样本均值和样本方差,则 $\frac{(n-1) s^2}{\sigma^2} \sim$
$\text{A.}$ ${\chi}^2(n-1)$
$\text{B.}$ $\chi^2(n)$
$\text{C.}$ $t(n-1)$
$\text{D.}$ $t(n)$
设随机变量 $X_1, X_2, \cdots, X_{100}$ 独立同分布, $E\left(X_i\right)=0, D\left(X_1\right)=1, i=1,2, \cdots, 100$,则由中心极限定理得 $P\left\{\sum_{i=1}^{100} X_i \leq 10\right\}$ 近似于
$\text{A.}$ 0
$\text{B.}$ $\Phi(1)$
$\text{C.}$ $\Phi(10)$
$\text{D.}$ $\Phi(100)$
二、填空题 （共 10 题, 每小题 2 分，共 20 分）
掷一颗骰子, $A$ 表示 “出现奇数点”, $B$ 表示 “点数不大于 3 ”, 则 $A-B$ 表示
设 $A, B, C$ 是三个随机事件,
$
P(A)=P(B)=P(C)=\frac{1}{4}, P(A C)=\frac{1}{6}, P(A B)=0, P(B C)=0,
$
则 $A, B, C$ 至少发生一个的概率为
袋中有 4 个球,其中有 2 个白球和 2 个黑球, 从中任意取出 2 个球,如果取出的 2 个球中恰好是 1 个白球和 1 个黑球就停止试验,否则将这 2 个球放回袋中重新抽取 2 个球, 直到取到 1 个白球和 1 个照球为止. 用 $X$ 表示抽取次数, 则数学期望 $E X=$
从数字 $1,2, \cdots, 10$ 中有放回地任取 4 个数字, 则数字 10 恰好出现两次的概率为
设随机变最 $X$ 服从参数为 2 的泊松分布, 则 $E(2 X)=$
设随机变量 $X \sim N(1,4)$, 则 $D(X)=$
设 $x_1, x_2, \cdots, x_{10}$ 为来自总体 $X$ 的样本, 且 $X \sim N\left(1,2^2\right), \bar{x}$ 为样本均值,则 $D(\bar{x})=$
在单边假设检验中, 原假设为 $H_0: \mu \leq \mu_0$, 则其备择假设为 $H_1$ :
设总体 $X$ 服从正态分布 $N\left(\mu, \sigma^2\right)$, 其中 $\sigma^2$ 未知, $x_1, x_2, \cdots, x_n$ 为其样本. 若假设检验问题为 $H_0: \mu=\mu_0, H_1: \mu \neq \mu_0$, 则采用的检验统计量表达现应为
设一元线性回归模型为 $y_i=\beta_0+\beta_1 x_i+\varepsilon_i, i=1,2, \cdots, n$, 则 $E\left(\varepsilon_i\right)=$.
三、解答题 （ 共 5 题，满分 50 分 ）
某种电子元件的寿命 $X$ 是随机变量, 其概率密度为
$$
p(x)=\left\{\begin{array}{cl}
\frac{C}{x^2} & x \geq 100 \\
0 & x < 100
\end{array}\right.
$$
求 (1) 常数 $C$;
(2) 若将 3 个这种元件串联在一条线路上, 试计算该线路使用 150 小时后仍能正常工作的概率。
某种电池的寿命（单位: 小时）是一个随机变量 $X$, 且 $X \sim N\left(300,35^2\right)$ 。
求（1）这样的电池寿命在 250 小时以上的概率;
（2） 求$a$ 使电池寿命在 $(300-a, 300+a)$ 内的概率不小于 0.9 。
设随机变量 $X \sim U\left[\begin{array}{ll}1, & 2\end{array}\right]$ 。
求 $Y=e^{2 X}$ 概率密度 $p_Y(y)$ 。
若随机变量 $X$ 服从泊松分布, 即 $X \sim P(\lambda)$, 且知 $E X^2=2$ 。求 $P\{X \geq 4\}$
设随机变量 $X$ 的概率密度为
$$
p(x)=\frac{1}{2} e^{-|x|}(-\infty < x < +\infty)
$$
求 $E X$ 和 $D X$ 。
设随机变量 $X$ 服从参数为 2 的指数分布。
证明: $\bar{Y}=1-e^{-2 X}$ 在区间 $(0,1)$ 上, 服从均匀分布。