一、解答题 (共 13 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
1. 计算:
2. 已知 , 则
3. 已知 , 求 的值。
4. 若 , 则 的最大值是
5. 设 或者 . 令
(1) 能否等于 2013 ? 证明你的结论;
(2) 能取到多少个不同的整数值?
6. 已知 , 则
7. 若实数 满足 , 代数式 的最大值是
8. 求所有的正整数 满足方程 .
9. 已知实数 满 足 , 则
10. 若实数 满足 , 求 的值.
11. 设 是正整数, 且使得 是完全平方数, 求 的值.
12. 阅读下列两则材料, 回答问题
材料一: 我们将
与
称为一对“对偶式”
因为
, 所以构造“对偶式”相乘可以有效地将
和
中的“
”去掉
例如: 已知
, 求
的值.
解:
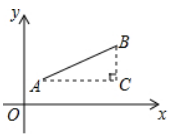
材料二: 如图, 点
, 点
, 以
为斜边作Rt
,
则
, 于是
, 所以
反之, 可将代数式
的值看作点
到点
的距离. 例如
所以可将代数式
的值看作点
到点
的距离.
(1) 利用材料一, 解关于
的方程:
, 其中
;
(2)①利用材料二, 求代数式
的最小值, 并求出此时
与
的函数关系式, 写出
的取值范围;
② 将①所得的
与
的函数关系式和
的取值范围代入
中解出
, 直接写出
的值.
13. 若 , 解方程